設備保全業務の最適化; メールマガジン

メールマガジン トップページ

トップページ > 設備保全管理ソリューション > FLiPS > メールマガジントップページ >
第10回：システム（系や系統）の評価とCMMS／EAMによる管理

参考：ワイブル分析を用いた故障分析

2014-09-01

戻る
本文（第10回）もご参照下さい

本説明では、ワイブル分析を説明します。 ワイブル分析は、故障情報を入力とし、不信頼度を求める手法です。 不信頼度が判れば、故障率、信頼度及び故障確率密度も知ることができます （｢故障率と信頼度の関係｣を参照）。

ワイブル分析

ワイブル分析を説明するために、以下の状態を考えます。 機器（全て同機種、同じような環境、負荷状況も似ている）が８台存在するとします。 ８台の機器について故障管理を行っているものとします。８台の機器の故障履歴を参照すると以下のとおりとなっているとしましょう。

故障情報

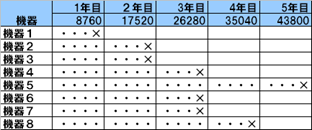
図１  故障情報


図１中の×印は、故障を表します。｢・・・｣は、正常に稼働していることを表します。機器１は、１年目で故障、機器２は、２年目で故障の様に機器８まで管理が出来ています。 故障の状況を評価するために、上図の状況をヒストグラムで表すと以下のとおりとなります。

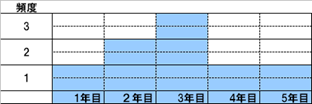
故障件数ヒストグラム

図２  故障件数ヒストグラム


１年目に１台が故障、２年目に２台、３年目がピークで３台壊れています。 この故障数に関するヒストグラムを一般化して表します。まず、考えられるのは、故障を正規分布として考える場合は、以下のとおりとなります。

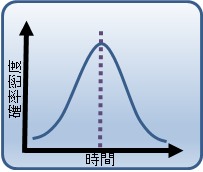
故障数正規分布近似

図３  故障数正規分布近似


横軸は、時間です。タテ軸は、発生確率密度です。 中心（ピーク）は、３年目に存在し、左右にすそ野が広がっています。 ここで、問題が発生します。 正規分布を用いて、故障の発生数を近似する場合、中心を境にして両側（左右）が同じ確率になっています。機器の故障は、弱いところから壊れるなど、偏りが存在するため、正規分布の様な左右対称ではなく、偏りを表現できた方が実際の故障発生数に沿ったものとなります。故障の発生数の偏りを表現するために、故障分析ではワイブル分布を用います。

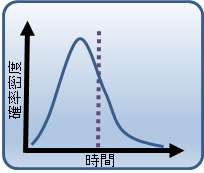
故障数ワイブル分布近似

図４  故障数ワイブル分布近似


ワイブル分布を用いることで、故障の発生数の偏りを考慮した故障確率密度として表現できる様になります。 ｢故障率と信頼度の関係｣で説明したように故障確率密度が判ると不信頼度を求めることが出来ます。 不信頼度は、故障確率密度の累積です。 以下に、図４を累積することで得られる不信頼度を示します。

不信頼度

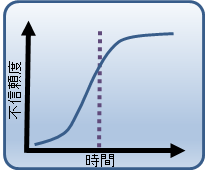
図５  不信頼度


図５の横軸は、時間、縦軸は、不信頼度（故障確率密度の累積）です。 本不信頼度グラフを用いることで、時間が特定できれば、すでに故障している機器の確率（数量）を知ることが出来ます。 本情報は、CMMS/EAMに登録された故障情報から求めた不信頼度です。 保全計画を策定する時に、いつごろ、何%が壊れるのかの推定に用いることが出来ます。 図５（不信頼度のグラフ）を作成するのは大変ですので、工学上は、以下の方法でワイブル近似を実施します。 図５（不信頼度のグラフ）の不信頼度曲線が直線になるように横軸、縦軸を座標変換し、グラフを書き直すと以下のとおりとなります。これを確率紙と呼びます。

確率紙

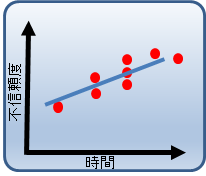
図６  確率紙


実際の手順は、今までの説明を前提として、次のとおり実施します。 各機器の故障までの時間を昇順に並べ、累積値を確率紙の上にプロット（図６中の赤い点）します。確率紙上へのプロットが終了したら平均となるような直線を適当に選んで引きます（最小二乗法）。この直線が不信頼度となります。 すなわち座標を元に戻せば、図５に示した不信頼度となり、微分したものは、 図４の故障確率密度になります。 不信頼度と故障確率密度が判れば、故障率のグラフを描くこともできます。 故障率は、故障確率密度を信頼度で割れば算出できます。信頼度は、１−不信頼度で計算できます。ただし、何れの指標も時間の関数となっているため、手動で実施すると大変です。 この手順もソフトウェアツールを用いると簡単に実施できます。 以下に弊社で販売しているAvailability WorkbenchのWeibull分析モジュールの例を示します。

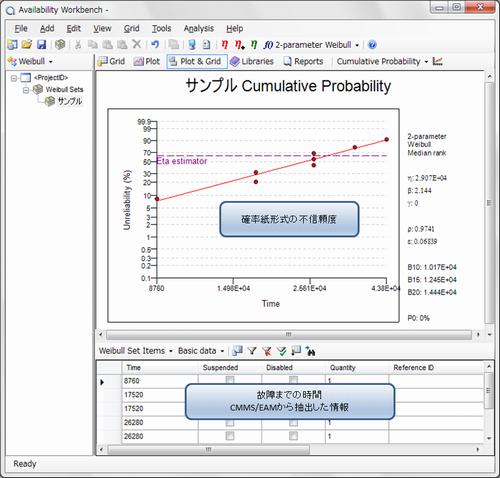
ワイブル分析ツール クリックして拡大表示

図７  ワイブル分析ツール（確率紙）


図７は、確率紙形式の不信頼度（故障確率密度の累積）です。 ツールを用いると、不信頼度の他に、 故障率や故障確率密度も簡単に参照できます。 以下に故障率と故障確率密度を示します。

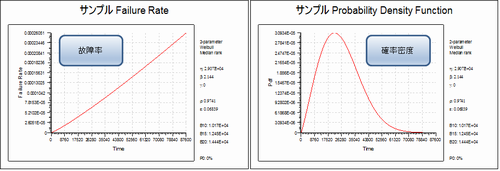
ワイブル分析ツール クリックして拡大表示

図８  ワイブル分析ツール（故障率、確率密度）


図８を参照すると、グラフの横にη（特性寿命パラメタ）、β（形状パラメタ）に関する情報が参照できます。 ワイブル分析では、このパラメタが重要となります。βは、約２となっています。 この場合、図８の故障率の様に単調増加の傾向を示します。βが２より大きくなればなるほど摩耗故障の特徴を示すようになります。 そして、βは、TBMの実施判断基準として用いることができます。 また、｢故障率と信頼度の関係｣で説明したB-Life値もグラフの右側に 計算されています。B10（不信頼度が10%に到達するまでの時間）は、1.017E4時間（約１．２年）が報告されています。 等の評価を進めていくことが可能になります。

ワイブル分析における留意点

本説明では、故障情報を元にワイブル分析を行う場合を説明しました。 ところが、プラントや市場に展開している製品では、統計処理ができるほど故障情報が集まらないことは、多々あります。 また、計画的に保全を実施している場合、故障が発生する前に機器の更新等を実施し、故障するまで機器を使っていない場合もあります。 故障情報が少ない場合（または存在しない場合）は、故障しないで作動している時間（生存期間に関する情報）を用いることが出来ます。 寿命の推定には、最尤法(※１)を用います。また、エンジニアリング的に劣化の進み具合が判っている場合や、似たような機器の劣化の進み具合が得られる場合、この値を用いることが出来ます。 これをワイベイズ法といいます。
ワイブル分析を実施する際に、故障情報が少ない場合（または存在しない場合）、最尤法やワイベイズ法を組み合わせて故障分析を行う必要があります。

さらに、故障情報は少ないが、不適合に関する管理等を実施している場合、不適合の内容を整理し、ワイブル分析を用いることで、不適合が発生する確率として扱うことができます。 保全計画を策定するという観点からは、不適合発生時期が推定できるということは、保全周期を決める上での重要な手掛かりになります。 言い換えると、保全計画策定における故障とは、何を持って故障とするかを検討するのが肝要と思われます。

※１　例えば、10台の車が存在し、１台は、2年目で壊れて修理、 他の9台は、5年間、問題なく使えている場合、 寿命は2年ではなく、残りの9台が5年間、故障もなく利用できていることを考慮に入れる 必要があります（壊れていない情報も寿命計算に含める）。

まとめ

本説明では、故障情報を元に、ワイブル分析を行うことを説明しました。 CMMS/EAMで故障情報を管理している場合に、有効な手順であり、手法もシンプルです。 実際の使用環境、負荷状況（運転情報）と組み合わせて、ワイブル分析結果を整理しておくことで、機器の癖（故障率や不信頼度）をデータベース化しておくことが出来ます。 機器の故障率や不信頼度をデータベース化しておくことで、 色々な機器の組み合わせとして表されるシステムの不信頼度が推定できる様になります。

戻る
本文（第10回）もご参照下さい