コラム - プラズマ・流体シミュレーションの基礎

ウェーブフロントではプラズマ, 希薄流体, 熱流体が解析可能なシミュレーション・ソフトウェアを多数扱っております。 本頁では, 初学者向けに数値解析・物理学関連の頻出用語を簡易的にまとめました. より詳細な内容, または各分野に特化した内容につきましては 別の記事 もご覧ください. これらの内容がシミュレーションの理解の助けとなれば幸いです.

記載内容 (頁内リンク)

1. 流体シミュレーションの一般的な手順
2. シミュレーションソフトウェア比較表
3. 粒子モデルと流体モデル
4. 低温プラズマと熱プラズマ
5. 気体の希薄度と分子流/連続流
6. 熱平衡と非平衡
7. 関連項目

PDF版

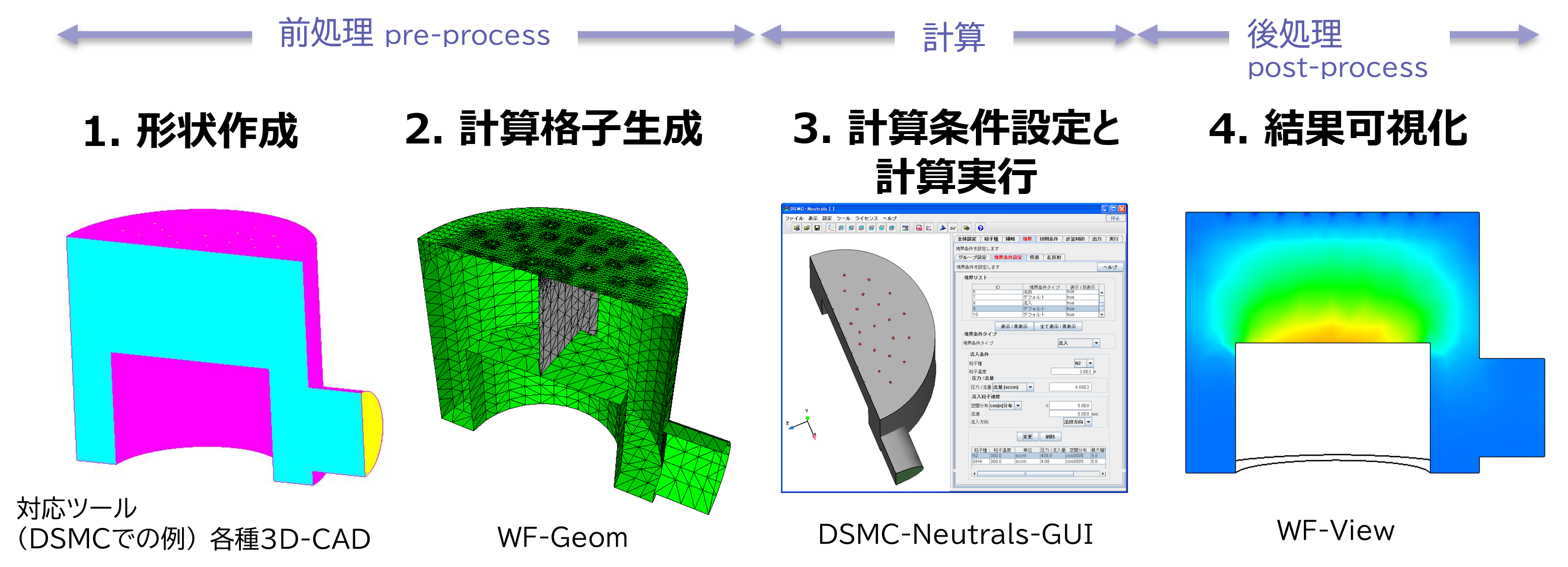
• プラズマ, 希薄流体, 熱流体の解析では, いずれも上記と同様の手順を踏む.
• シミュレーション対象の空間領域内に 計算格子 (mesh) が必要.
• 密度, 流速, 温度といった変数は, 計算点や要素中心の位置で定義される.
• これらの量を数値的に求める事が流体シミュレーションの目的となる.
• 計算格子は解の数値精度, 空間解像度, 計算時間 等に強く影響する.

ソフトウェア	特長	適用例
DSMC-Neutrals 粒子モデルによる希薄気体解析	流体モデルが適用できない高真空下のガス流れ解析に特化. 分子流領域における気体分子の挙動を実現象に近いモデルで再現.	半導体製造装置(化学蒸着, 真空蒸着, 分子線エピタキシー), HDD装置
Particle-PLUS 粒子モデルによるプラズマ解析	流体モデルが適用できない低温プラズマ解析に特化. 複雑な電磁場や壁近傍における電子やイオンの運動を正確に計算. DSMC-Neutralsとほぼ同等の中性気体流れの計算機能に加えて, 様々なスパッタリング計算モデルも搭載.	半導体製造装置(マグネトロンスパッタリング, イオンプレーティング, 電子ビーム蒸着, 酸素アッシング), 宇宙推進機
Particle-PLUS/DL 深層学習による プラズマ計算代理モデル	深層学習とCAEを融合したプラズマ解析. 高速計算でパラメトリックスタディを実現.	半導体製造装置(ICP等)
VizGlow 流体モデルベースのプラズマ解析	CCP, ICP, マイクロ波プラズマ, 大気圧プラズマ等の幅広いプラズマ解析に対応. ICPやマイクロ波プラズマを高速に計算するための近似モデル. 粒子モデルとの連成で粒子の帯電も計算可能.	半導体製造装置(PECVD, ICP-RIE), 自動車用コーティング装置, スパークプラグ
VizSpark 流体モデルによる熱プラズマ解析	アークプラズマの解析に特化. 固体との共役熱伝達, 磁場や流れとの連成も考慮可能.	溶射, 遮断機, プラズマ切断機, 大気圧スパークプラグ, HIDランプ
SimericsMP+ ポンプ/バルブ特化型熱流体解析	特に容積型ポンプ, バルブ, コンプレッサーの解析に強みを持っており, メッシュ生成機能が強い.	自動車関連, 建設機械, 冷凍/空調関連

• ウェーブフロントのソフトウェア製品の一部を記載している.
• CAE関連製品全般に関しては こちらの頁 を参照.

	粒子モデル (代表粒子近似)	流体モデル (連続体近似)
具体的な手法	DSMC, PIC, Test-Particle 等	FVM, FEM 等
基礎方程式	粒子の運動方程式 *1	流体の輸送方程式 *2
基礎変数	粒子の位置と速度	流速と熱力学的状態量 (密度, 圧力, 内部エネルギー 等)
速度分布の仮定	無し 任意の速度分布を正確に扱える.	局所熱平衡 特定の速度分布が仮定される. *3
衝突/輸送計算の 使用変数	衝突断面積	輸送係数 (移動度と拡散係数)
適用の目安	分子流 ～ 中間流 *4	連続流
計算精度や計算負荷に 大きく影響する設定	計算粒子数 計算時間幅	計算格子の幅と形 計算時間幅

1. 計算粒子が十分に多い場合はBoltzmann方程式と等価になる.
2. 物質量輸送方程式(連続の式), 運動量輸送方程式, エネルギー輸送方程式から成る連立方程式を指す. 各種輸送方程式はBoltzmann方程式について速度モーメントを取る事で導出される[参考記事a]. なお連立方程式の構成によっては, 系を閉じるための補助式として状態方程式も必要となる[参考記事b].
3. 有名なものとして(shifted-)Maxwellian分布, 電子に対するDruyvesteyn分布がある.
4. 中間流領域に対しては, 計算負荷の観点から流体モデルが選択される事も多い.

要点

• 低温プラズマやプラズマシース, 希薄流れ(分子流)では, 速度分布がマクスウェル分布から外れる可能性がある. これらの現象は 粒子モデル で精度良く解析できる. また表面の作用を受けやすい壁近傍の流束・エネルギー分布・角度分布の解析にも粒子モデルは有用である.
• 一方で, 圧力が高くなり熱化が十分に進行すると, 速度分布はマクスウェル分布に近づく. そのような場合は 流体モデル で解析可能となる. 一般的に, 同等の計算格子を用いる場合, 流体モデルは粒子モデルほど計算負荷は大きくならない.

具体例

• 圧力 1 Pa, 温度 300 K のアルゴンガスが口径 1 cm の流路を通る場合, クヌーセン数は 0.5 ～ 0.7 程度である. この程度の希薄度であれば粒子モデルでの解析が提案される.

低温プラズマ

低圧で衝突頻度が低いプラズマでは, 電子集団のエネルギーは高い状態に維持されるが, イオンはほぼガス温度(室温)に近い状態に保たれる. このように熱的に非平衡な状態になっているプラズマを 非平衡プラズマ, あるいはガス温度が低いという意味で 低温プラズマ という. 非平衡プラズマ中では, 粒子の部分集団の速度分布がマクスウェル分布になっているとは限らない.

熱プラズマ

圧力が上昇すると衝突頻度が増加するため, 電子・イオン・ガスの温度は相互に近づき, 大気圧付近では数千度の温度で一致するようになる. このような熱平衡状態にあるプラズマを 熱平衡プラズマ あるいは単に 熱プラズマ という. 定常的な熱プラズマ中では, 粒子集団の速度分布は温度で規定されるマクスウェル分布に従う.

1. 参考文献
2. 日本学術振興会 プラズマ材料科学第153委員会 編,「大気圧プラズマ -基礎と応用-」, オーム社 (2009)
3. 電気学会 編, 電気学会大学講座「プラズマ工学」, オーム社 (1997)
4. 真壁利明, 応用物理 (1991) 60巻, 7号, p.663-673

気体の流れは希薄度によって分子流・連続流・中間流のように分類される. 希薄度の指標としては平均自由行程とクヌーセン数がよく使用される.

平均自由工程 (mean free path)

気体分子1つが他の分子と衝突した後, 次に衝突するまで飛行する平均距離のことを 平均自由行程 といい, 記号 λ 等で表す. 圧力が低いと衝突頻度は低くなるため λ は長くなる. 例として, 圧力 1 Pa, 温度 300 K におけるアルゴンガスの λ は 5 ～ 7 mm 程度である. 数値のブレは衝突断面積の与え方に依るものである.

クヌーセン数 (Knudsen number)

「流れを連続体として扱えるかどうか」を示す無次元数として クヌーセン数 が定められている. 記号には Kn が用いられる. 空間領域の代表的な長さ L とするとき, 次で計算される. \begin{align*} {\rm Kn} = \frac{\lambda}{L} \end{align*}

分子流 (molecular flow)

0.3 < Kn の場合, 分子同士の衝突よりも分子と壁との衝突が支配的となる. 壁に衝突するまで分子は自由に飛行できる事から, このような流れを 自由分子流 あるいは単に 分子流 という. なお Kn の境界値については, 文献によって差異が見られる. 分子流領域にある原子や分子は, 一般的に気体分子運動論によって記述される.

連続流 (continuous flow)

Kn < 0.01 の場合, 分子同士の衝突により熱平衡状態になるため, 個々の分子運動よりも統計集団としての状態が支配的となる. すると連続流体として扱うことができ, このような流れを 連続流 という. この領域では分子間衝突による粘性も生じるために 粘性流 とも呼ばれる.

中間流 (intermediate flow)

分子流と連続流の間の領域を 中間流 または 遷移流 という.

1. 参考文献
2. 日本機械学会 編,「原子・分子の流れ 希薄気体力学とその応用」, 共立出版 (1996)
3. 日本機械学会 編, コンピュータアナリシスシリーズ7, 「原子・分子モデルを用いる数値シミュレーション」, コロナ社 (1996)
4. 吉田肇, 武井良憲, 新井健太, 表面と真空 (2020) 63巻, 6号, p.304-310

熱平衡状態と状態量

十分な衝突により粒子集団が熱平衡状態にあるとき, 個々の粒子の位置や速度といった微視的変数を調べなくても, 密度・圧力・内部エネルギー(温度) といった巨視的変数, いわゆる 状態量 で集団を記述することができる (by熱力学). また, これらの状態変数を用いて流れを記述する際は, 局所的に熱平衡状態である事が仮定されている (by流体力学).

マクスウェル分布 (Maxwellian distribution)

静止した熱平衡状態にある粒子集団の速度分布は マクスウェル分布 をとる (by平衡統計力学). 流れがある場合は, 分布全体が流速分だけ平行移動していると考えれば良く, シフト-マクスウェル分布と呼ばれる事もある. 温度 T, 流速 $\vec{u}$ の状態にある粒子集団に対して, 分布関数 f は次式で表される. \begin{align*} f(\vec{v}) = \left( \frac{m}{2\pi kT} \right)^{3/2} \exp \left[ -\frac{m(\vec{v}-\vec{u})^2}{2kT} \right] \end{align*} ここで, $\vec{v}$ は粒子の速度, m は粒子の質量, k はボルツマン定数である.

ボルツマン方程式 (Boltzmann equation)

非平衡状態も含めた粒子集団の運動は次式の ボルツマン方程式 で記述される (by運動論). \begin{align*} \frac{\partial f}{\partial t} + \vec{v} \cdot \nabla f + \frac{\vec{F}}{m} \cdot \nabla _{v} f = \left( \frac{\delta f}{\delta t} \right)_{\rm \! C} \quad , \quad f = f(\vec{v}, \vec{r}, t) \end{align*} ここで, $\vec{F}$ は外力であり, 右辺にある添字 C は衝突項(散乱項)である事を示す. f は速度 $\vec{v}$, 位置 $\vec{r}$, 時刻 t を変数に持つ分布関数である. ボルツマン方程式は6次元位相空間内の時間発展を記述しており, これを気体分子の数 (アボガドロ数オーダー) 個について解くのは容易ではない. そこで通常は粒子モデルや流体モデルを用いて近似される [参考記事c].

1. 参考文献
2. Michael A. Lieberman，Allan J. Lichtenberg 著，「プラズマ／プロセスの原理」, 第2版, 丸善 (2010)
3. 高村秀一 著, 「プラズマ理工学入門」, 森北出版 (1997)