Particle-PLUS コラム - プラズマモデリング(連載) - 第4回
ウェーブフロントでは「粒子法」でプラズマをモデル化したシミュレーションソフトウェア『Particle-PLUS』や 「流体法」のプラズマシミュレーションソフトウェア『VizGlow』を取り扱っており, これらを適宜使い分けながら皆様方へ長年ソリューションを提供しております. 本コラムを読んでプラズマシミュレーションに少しでも興味をお持ちになりましたら 資料請求や 無料セミナーなど承りますので, いつでもお気軽にお問い合わせください.
前回までは, プラズマを流体モデル化した場合の支配方程式系を導出しました. しかしながら,方程式を閉じた系にするためには
- 電磁場
- 応力と熱流束
- 散乱項
2. 応力と熱流束の決定のための近似Approximations for stress and heat flux decision
流体としてのプラズマの運動を記述する流体方程式, \begin{align} & \frac{\partial n_{s}}{\partial t} + \vec{\nabla}\cdot\vec{\varGamma}_{s} = S_{s}, \label{eq_fluid_1} \\ & \frac{\partial}{\partial t}\left(\rho_{s}\vec{u}_{s}\right) + \nabla \cdot \left\{ \rho_{s}\left(\vec{u}_{s}\otimes\vec{u}_{s}\right) \right\} = q_{s} n_{s} \left(\vec{E}+\vec{u}_{s}\times\vec{B}\right) - \nabla \cdot {\bf{P}}_{s} + \vec{K}_{s}, \label{eq_fluid_2} \\ & \frac{\partial}{\partial t}\left(n_{s}\varepsilon_{s}+\theta_{s}\right) + \nabla \cdot \left\{ \left(n_{s}\varepsilon_{s}+\theta_{s}\right)\vec{u}_{s}+\left(\vec{u}_{s}\cdot{\bf{P}}_{s}\right)+\vec{Q}_{s} \right\} = q_{s} n_{s} \left(\vec{u}_{s}\cdot\vec{E}\right) + H_{s} \label{eq_fluid_3} \end{align} の式中に現れる高次モーメント量である応力と熱流束を決定する方法として,
- 応 力:系が満たす状態方程式を仮定(=応力 ${\bf{P}}_{s}$ を密度 $n_{s}$ や温度 $T_{s}$ の関数として記述する)
- 熱流束:$\vec{Q}_{s}=0$ を仮定
- 熱流束:Fourierの法則 $\vec{Q}_{s}=-\kappa_{s}\nabla T_{s}$ により熱流束を計算(熱伝導率 $\kappa_{s}$ は物性値)
第2章では,これらの近似の物理的意味や,モデル化により解くべき流体方程式系 (\ref{eq_fluid_1})–(\ref{eq_fluid_3}) がどのように変更されるかを 詳しく調べていきましょう.
2.1. 準熱平衡近似Quasi-equilibrium approximation
2.1.1. 等方性分布と等方性応力
分かりやすい近似として,考えているプラズマを準熱平衡状態にある理想気体として扱う方法があります.
具体的にはまず,粒子種 $s$ は局所平衡状態にあり,その速度分布関数 $f_{s}$ が局所的に等方性分布であると仮定します.
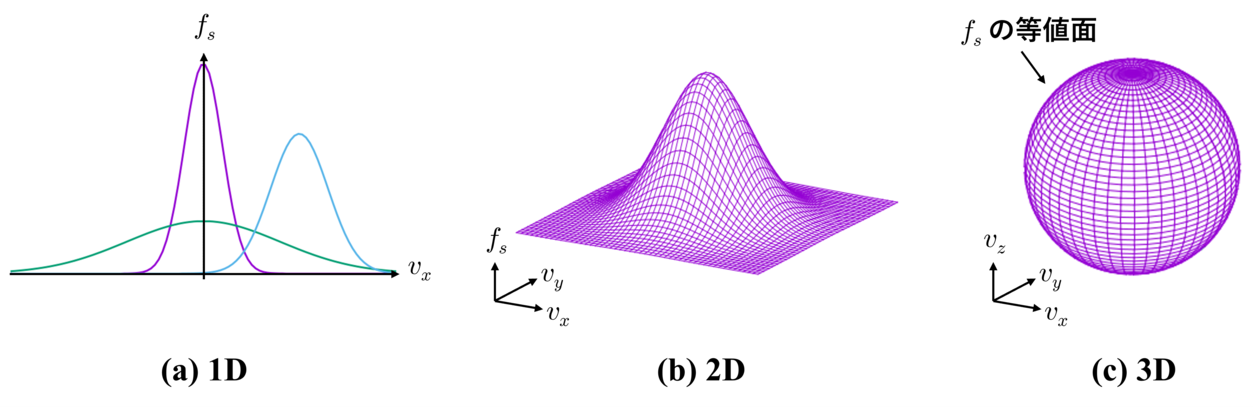
▲ 等方性分布関数の例. 熱平衡速度分布であるMaxwell分布(Maxwell-Boltzmann分布)は代表的な等方性分布です. ここでは広義の局所平衡性として,分布の中心が定数だけずれている(即ち $|\vec{u}_{s}|\neq 0$ である)shifted-Maxwell分布の場合も含めます. (a) 1次元等方性分布. (b) 2次元等方性分布. (c) 3次元等方性分布.速度分布 $f_{s}$ の等値面は速度空間上の球殻です.
等方性速度分布を仮定した場合,応力もまた等方的であり, \begin{align} \text{$ij$ 成分: } ({\bf{P}}_{s})_{ij} = p_{s}\delta_{ij} \label{eq_pressure}\\ \end{align} のように書けます.
以上のことから,等方性の速度分布(=準平衡速度分布)の仮定により理想気体の状態方程式 \begin{align} p_{s} = \frac{1}{3}\mathrm{tr}{\bf{P}}_{s} = n_{s}k_{\mathrm{B}} T_{s} \label{eq_ideal} \end{align} が成り立つことが導けます*3.
したがって,以下のような準熱平衡近似における流体方程式が得られます.
これで,流体方程式を連立して解くには過剰な未知数であった応力 ${\bf{P}}_{s}$ と熱流束 $\vec{Q}_{s}$ を消すことができました.
*1 例えば,Maxwell分布の場合であれば計算は簡単です. 分布関数の規格化に関連する適当な係数を $\eta$ と書くと,$\vec{v}=\vec{w}_{s}+\vec{u}_{s}$ であり, そのJacobianは $\mathrm{d}\vec{v}=\mathrm{d}\vec{w}_{s}$ ですので, \begin{align*} \text{$i$ 成分: } (\vec{Q})_{i} = (\langle (\vec{w}_{s}\cdot\vec{w}_{s})\vec{w}_{s} \rangle)_{i} \propto \sum_{j=1}^{3}\prod_{k=1}^{3} \int w_{sj}^{2}w_{si}\mathrm{e}^{-\eta v_{k}^{2} }\mathrm{d}v_{k} = \sum_{j=1}^{3}\prod_{k=1}^{3} \int w_{sj}^{2}w_{si}\mathrm{e}^{-\eta\left(w_{sk}+u_{sk}\right)^{2}}\mathrm{d}w_{sk} =0 \end{align*} となります*2. 最後の等式は,非積分関数が奇関数であることを用いました. (一般化されたGauss積分の公式を知っていれば自明な結果です.)
*2 ここでは,空間に関する3次元ベクトルの成分を $1,2,3$ のように書きました(例:$\vec{w}_{s}=(w_{s1},w_{s2}.w_{s3})$). これは,成分を下付き文字 $x,y,z$ で表すよりも,和および積の記号を使う際に都合が良かったからなのですが, 本連載を通して $(A_{x},A_{y},A_{z})$ のような書き方と混在することになってしまいました. 読者の皆様をこれによって迷わせることはないと考えておりますが, これら2通りの表記の使い分けに特に深い意味はないことを申しあげておきます.
*3 もしかすると,一般的な理想気体の状態方程式(\ref{eq_ideal})が成り立つ系を考えているのに,エネルギー方程式中の全エネルギー
$n_{s}\varepsilon_{s}+\theta_{s} = n_{s}\varepsilon_{s}+(3/2)n_{s}k_{\mathrm{B}}T_{s}$
に振動と回転運動の内部エネルギー分が含まれていないことにムズムズしている方がいるかもしれません.
(エネルギー方程式の導出の際に並進+熱エネルギー $(m_{s}|\vec{v}|^{2}/2 = m_{s}|\vec{u}_{s}+\vec{w}_{s}|^{2}/2)$
だけを作用して速度モーメントを計算したから当たり前なのですが.)
しかしながら,実用上は下記の理由により,ここでは粒子の並進運動の自由度分のみを考えれば良いことに注意してください.
回転と振動運動による内部エネルギーの増減は非弾性衝突に伴う励起現象に起因します.
言い換えると,並進+熱エネルギーとそれ以外の内部エネルギーは非弾性衝突を通じてのみ交換します.
一方で,シミュレーションを行う上でモード(回転準位や振動準位)が異なる粒子種は別々の粒子種として扱うことが望ましいという都合があります.
(例えば,原子 $\mathrm{A}$ と励起種 $\mathrm{A}^{\ast}$ の存在分布をそれぞれ求めたい場合には,
それらを互いに異なる粒子種として扱い,それぞれに対して流体方程式を解く必要があります.)
以上のことから,左辺に含まれるはずの回転+振動の内部エネルギーの対流分と
右辺のエネルギー交換項 $H_{s}$ に含まれるはずの衝突による内部エネルギーの増減分はキャンセルできるので,
エネルギー方程式(\ref{eq_isotropic_fluid_eq3})に関してそれらの内部エネルギーを陽に含まない形で書き下しても実用上問題ありません.
2.1.2. 準熱平衡な速度分布が意味すること
ここで考えている準熱平衡,言い換えれば等方的な速度分布は何を意味しているのでしょうか.
この項で述べることは熱力学を学んだ方にとっては当たり前の内容ではあるのですが,
低温プラズマ,特にその粒子間衝突を考えるうえで重要な知見を含んでいますので一度おさらいしておきましょう.
気体の速度分布は熱平衡状態においてMaxwell分布と一致します.
これは空間的に完全に等方的な速度分布です.
一定の流速があり分布の中心が平行移動する場合にはshifted-Maxwell分布を考えたり,
強電場下での電子の速度分布としてDruyvesteyn分布と呼ばれる分布関数を考えることがあります.
(後で述べた2つの速度分布も,平均速度からの分布関数の広がり方が空間的に等方的です.)
このような等方的な速度分布を実現する状況は,
同一の速度分布の下で運動する粒子種間の弾性衝突による熱化(thermalisation)が,
異なる速度分布を持つ粒子種間の衝突や電場による加速などのエネルギー変化と比べて速く支配的である場合です.
(なお,粒子の速度分布の熱化の速さについては次回のコラムで解説します.)
また,等方的な速度分布を仮定した時点で自然と $\vec{Q}_{s}=0$ が導かれたことに注目しましょう.
これはつまり,熱平衡状態にあるプラズマ粒子群の運動は熱の移動を伴わない(=等熱的)ことを意味しています.
このことから,理想気体の状態方程式(\ref{eq_ideal})は等熱的なプラズマの熱力学的関係式だと言えそうです.
議論が散らかってきたところで一旦まとめますと,一言でプラズマが準熱平衡状態にあるといった場合,
暗に次の状況が仮定されていると考えられます.
- 空間的に等方的な速度分布
- 同一速度分布を持つ粒子との弾性衝突が支配的要因となる素早い熱化
- 等熱性 $\vec{Q}_{s}=0$
- 理想気体の状態方程式(\ref{eq_ideal})
第4回まとめ
第4回では,準熱平衡近似の下での流体方程式について考察しました. 準熱平衡が意味する内容についても考え,その中で同一速度分布の粒子間の弾性衝突による熱化が速く支配的であることが重要であると述べました. このまま議論を続けるには長くなってまいりましたので, プラズマ中の粒子の熱化の緩和時間について議論は次回に行いたいと思います.
ウェーブフロントでは「粒子法」でプラズマをモデル化したシミュレーションソフトウェア『Particle-PLUS』や 「流体法」のプラズマシミュレーションソフトウェア『VizGlow』を取り扱っており, これらを適宜使い分けながら皆様方へ長年ソリューションを提供しております. 本コラムを読んでプラズマシミュレーションに少しでも興味をお持ちになりましたら 資料請求や 無料セミナーなど承りますので, いつでもお気軽にお問い合わせください.
 |
上野 崚一郎 | 博士(理学) 1991年 広島県生まれ 2019年 ウェーブフロント入社 2019年 広島大学大学院理学研究科 博士後期課程修了 学生時代は数値シミュレーションを使った素粒子論(格子ゲージ理論)の研究に従事. 入社後は,専門職(エンジニア)として希薄気体解析・プラズマ解析ソフトウェアの開発をはじめとして, 解析コンサルティング業務や国内外のユーザー向けの技術サポート・トレーニングなどを担当. 最後までお読みいただきありがとうございます. お気づきの点や扱ってほしい話題がございましたらお気軽にお問い合わせください. |
