Particle-PLUS コラム - プラズマモデリング(連載) - 第5回
ウェーブフロントでは「粒子法」でプラズマをモデル化したシミュレーションソフトウェア『Particle-PLUS』や 「流体法」のプラズマシミュレーションソフトウェア『VizGlow』を取り扱っており, これらを適宜使い分けながら皆様方へ長年ソリューションを提供しております. 本コラムを読んでプラズマシミュレーションに少しでも興味をお持ちになりましたら 資料請求や 無料セミナーなど承りますので, いつでもお気軽にお問い合わせください.
第4回で,プラズマが準熱平衡に至る過程では, 同一の速度分布で表せる粒子間の熱化が その他の(異なる速度分布の粒子間衝突や電磁場との相互作用による)エネルギーのやり取りよりも早く支配的であることが重要であると述べました. そこで,今回は熱化過程について詳しく考察していきましょう.
2.1.3. 異なる粒子種間衝突による熱化の時定数
準熱平衡分布が実現するためには,
その速度分布を異にする粒子種間の衝突による熱化(回りくどく言えば,衝突を通じたエネルギー交換による温度緩和)が
同一速度分布の粒子種間の熱化よりも遅い必要があります.
このことについて,高校物理の範囲で理解できる2体衝突のトイモデルを通して考えてみましょう.
質量 $m_{\mathrm{A}}$ の物体Aが質量 $m_{\mathrm{B}}$ の物体Bと完全弾性衝突する状況を考えます.
ここでは簡単のために,衝突前の物体Bの静止系を実験室系としておきます.
また,物体AおよびBの衝突前の速度を $\vec{v}_{\mathrm{A}}$ および $\vec{v}_{\mathrm{B}}=\vec{0}$,
衝突後の速度を $\vec{v}_{\mathrm{A}}^{\prime}$ および $\vec{v}_{\mathrm{B}}^{\prime}$ と書くことにします.
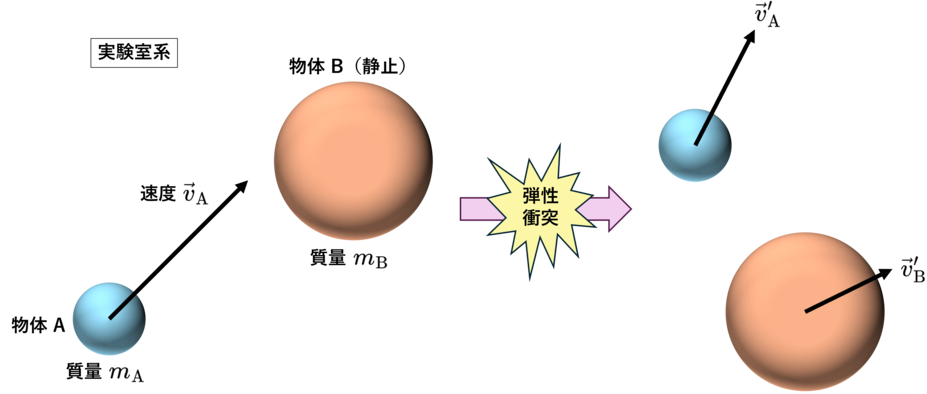
▲ 実験室系における弾性衝突の設定.
さて,この後の議論は角度 $\chi$ をそのまま使っても続けられるのですが,少し寄り道してこれを質量中心系における散乱角 $\theta$ に書き直します. (興味がなければ式(\ref{eq_mom_trans})まで飛ばしてください.)
さて,衝突前後の重心速度 \begin{align} \vec{v}_{\mathrm{G}} = \frac{m_{\mathrm{A}}\vec{v}_{\mathrm{A}}}{m_{\mathrm{A}}+m_{\mathrm{B}}},\quad \vec{v}_{\mathrm{G}}^{\prime} = \frac{m_{\mathrm{A}}\vec{v}_{\mathrm{A}}^{\prime}+m_{\mathrm{B}}\vec{v}_{\mathrm{B}}^{\prime}}{m_{\mathrm{A}}+m_{\mathrm{B}}} \end{align} および質量中心系における衝突前後の物体A,Bの速度 $\vec{c}_{\mathrm{A}}$,$\vec{c}_{\mathrm{B}}$,$\vec{c}_{\mathrm{A}}^{\prime}$,$\vec{c}_{\mathrm{B}}^{\prime}$ を用いると,実験室系の速度および運動量は \begin{align*} & \vec{v}_{\mathrm{A}}=\vec{c}_{\mathrm{A}}+\vec{v}_{\mathrm{G}}, && \vec{0}=\vec{c}_{\mathrm{B}}+\vec{v}_{\mathrm{G}}, && \vec{v}_{\mathrm{A}}^{\prime}=\vec{c}_{\mathrm{A}}^{\prime}+\vec{v}_{\mathrm{G}}^{\prime}, && \vec{v}_{\mathrm{B}}^{\prime}=\vec{c}_{\mathrm{B}}^{\prime}+\vec{v}_{\mathrm{G}}^{\prime}, \\ & m_{\mathrm{A}}\vec{v}_{\mathrm{A}} =m_{\mathrm{A}}\vec{c}_{\mathrm{A}} +m_{\mathrm{A}}\vec{v}_{\mathrm{G}}, && \vec{0} =m_{\mathrm{B}}\vec{c}_{\mathrm{B}} +m_{\mathrm{B}}\vec{v}_{\mathrm{G}}, && m_{\mathrm{A}}\vec{v}_{\mathrm{A}}^{\prime}=m_{\mathrm{A}}\vec{c}_{\mathrm{A}}^{\prime}+m_{\mathrm{A}}\vec{v}_{\mathrm{G}}^{\prime}, && m_{\mathrm{B}}\vec{v}_{\mathrm{B}}^{\prime}=m_{\mathrm{B}}\vec{c}_{\mathrm{B}}^{\prime}+m_{\mathrm{B}}\vec{v}_{\mathrm{G}}^{\prime} \end{align*} と表すことができます. ここで,弾性衝突においては運動量保存則(\ref{eq_mom_con})より,$\vec{v}_{\mathrm{G}}=\vec{v}_{\mathrm{G}}^{\prime}$ です.
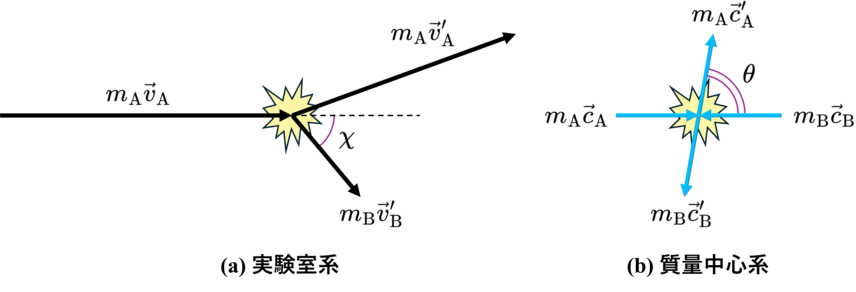
▲ 運動量ベクトルの関係. (a) 実験室系. (b) 質量中心系. 質量中心系の運動量保存則は $m_{\mathrm{A}}\vec{c}_{\mathrm{A}}+m_{\mathrm{B}}\vec{c}_{\mathrm{B}} =m_{\mathrm{A}}\vec{c}_{\mathrm{A}}^{\prime}+m_{\mathrm{B}}\vec{c}_{\mathrm{B}}^{\prime}=\vec{0}$ である.
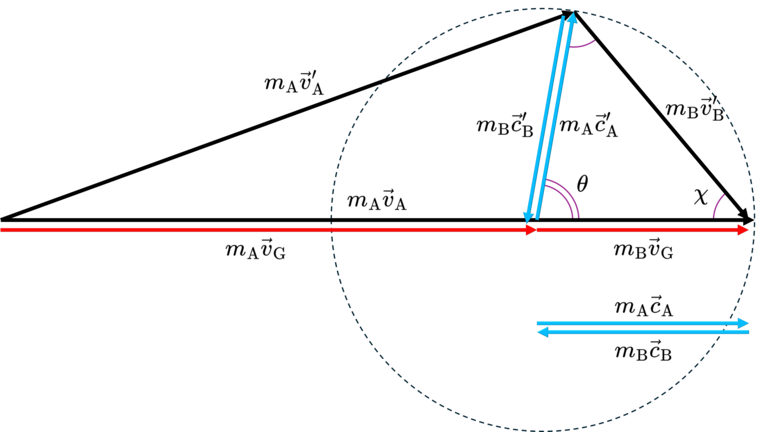
▲ 運動量ベクトルの幾何学的理解.
さて議論を元に戻しましょう. 式(\ref{eq_mom_trans})から,この衝突で物体Aから物体Bに移行したエネルギーの割合が, \begin{align*} \frac{\text{(衝突後の物体Bのエネルギー)}}{\text{(衝突前の物体Aのエネルギー)}} \equiv\frac{\Delta E}{E} = \frac{m_{\mathrm{B}}|\vec{v}_{\mathrm{B}}^{\prime}|^{2}}{m_{\mathrm{A}}|\vec{v}_{\mathrm{A}}|^{2}} = \frac{4m_{\mathrm{A}}m_{\mathrm{B}}}{(m_{\mathrm{A}}+m_{\mathrm{B}})^{2}}\sin^{2}\frac{\theta}{2} = \frac{2m_{\mathrm{A}}m_{\mathrm{B}}}{(m_{\mathrm{A}}+m_{\mathrm{B}})^{2}}\left(1-\cos\theta\right) \end{align*} のように物体AおよびBの質量 $m_{\mathrm{A}}$,$m_{\mathrm{B}}$ と散乱角 $\theta$ のみに依存する形で書けることが分かります*1.
以上より,このような衝突が起きるまでの平均自由時間を$\Delta t$とすると,衝突によるエネルギー緩和の時間依存性を \begin{align} \frac{\Delta E}{\Delta t} = - \left\{\frac{2m_{\mathrm{A}}m_{\mathrm{B}}}{(m_{\mathrm{A}}+m_{\mathrm{B}})^{2}}\left(1-\cos\theta\right)\right\} E \equiv - \frac{1}{\tau}E, \qquad \tau = \left\{\frac{2m_{\mathrm{A}}m_{\mathrm{B}}}{(m_{\mathrm{A}}+m_{\mathrm{B}})^{2}}\left(1-\cos\theta\right)\right\}^{-1} \end{align} のように表せることが分かります. この式は,物体同士の弾性衝突によるエネルギー緩和(=熱化)は, 互いの質量と散乱角のみに依存する時定数 $\tau$ による指数関数的な振る舞いをすることを表しています. この時定数 $\tau$ の値が小さい時ほど弾性衝突する2種類の物体は素早く熱化するのです.
以下では簡単のために $\cos \theta =0$ とします. 熱化の時定数 $\tau$ は,$m_{\mathrm{A}}=m_{\mathrm{B}}$ のときに $\tau=2$ になりますが, $m_{\mathrm{A}}\ll m_{\mathrm{B}}$ のとき(例えば,物体Aが電子,物体Bが背景ガスの場合)には $\tau\simeq m_{\mathrm{B}}/(2m_{\mathrm{A}}) \gg 1$ になります. この振る舞いは $m_{\mathrm{A}}\ll m_{\mathrm{B}}$ であっても同様です. これはつまり,質量が大きく異なる粒子種間の衝突による熱化は,同程度の質量をもつ粒子種間の熱化よりも遅いことを意味しています*2.
この項での話をまとめると,粒子間衝突が極めて多いような状況(=熱プラズマ)でなければ, 異なる質量を持つ粒子種同士(特に電子とイオン)はいずれ互いに独立な熱平衡分布に達すると考えられます. このことは,低温プラズマ(非平衡プラズマ)の定義,「電子とイオンが互いに異なる温度で運動しているようなプラズマ」と矛盾しません. そもそもの目的であるプラズマ粒子種ごとの流体方程式を解くという観点から言えば, 前回(2.1.2項)述べたように, 同一の速度分布を持つ粒子種同士の衝突によるエネルギー交換効率は 異なる速度分布を持つ粒子種同士のそれよりも速く支配的であるといえます.
衝突について厳密にいえば, 反応性のガス衝突やプラズマ粒子同士(特に電子と背景ガスあるいは電子とイオン)の衝突では非弾性衝突が無視できないため 必ずしも最終的な速度分布が熱平衡分布(Maxwell分布)に一致するとは限りません. しかしながら,そもそもプラズマプロセスで用いられるような低圧の弱電離プラズマであれば, 支配的な衝突の種類は多くの場合で弾性衝突であり, また,電子と背景ガス・イオンの衝突ならばそれらの質量差が非常に大きく時定数が大きい(=それらの熱化にはかなりの時間を要する)こともあり, 結局のところ粒子種ごとに独立に熱化していると考えて問題ないことが多いです.
*1 実験室系における物体Bの衝突前の速度を $\vec{0}$ としたので,衝突後の物体Bのエネルギーがそのまま全て物体Aから受け取ったエネルギーと等しくなります.
*2 逆に言えば,同程度の質量の粒子種同士(イオンと背景ガスなど)は,仮に異なる粒子種であったとしても(相対的に)素早く熱平衡に達すると考えられます. 実際の流体プラズマシミュレーションにおいてもイオン種に対するエネルギー方程式を解くことは稀であり, 通常は背景ガスと同一のエネルギー状態にあると仮定します.
2.1.4. 電磁場とのエネルギー授受と粒子の熱化
今度は,熱化した粒子群に対して電磁場が与える影響について統計力学的に考えてみましょう.
スカラーポテンシャル $\phi(\vec{x},t)$ およびベクトルポテンシャル $\vec{A}(\vec{x},t)$ が作る電磁場中を一様温度 $T$ で等方的に運動する
$N$ 個の理想気体荷電粒子(質量 $m_{i}$,電荷 $q_{i}$,位相 $(\vec{x}_{i}(t),\vec{v}_{i}(t))$;$i=1,2,\dots,N$)を考えます.
この系のHamiltonian $H[\vec{x}_{1},\dots,\vec{x}_{N},\vec{v}_{1},\dots,\vec{v}_{N};\phi,\vec{A}]$ は,
\begin{align*}
H & = \sum_{i=1}^{N}\left\{ \frac{m_{i}}{2} \left(\vec{v}_{i}-q_{i}\vec{A}\right)\cdot\left(\vec{v}_{i}-q_{i}\vec{A}\right) + q_{i}\phi \right\}
= \sum_{i=1}^{N}\left\{ \frac{m_{i}}{2} \left(\vec{v}^{\prime}_{i}\cdot\vec{v}^{\prime}_{i}\right) + q_{i}\phi \right\},
\\
\vec{v}^{\prime}_{i} & \equiv \vec{v}_{i}-q_{i}\vec{A}
\end{align*}
で与えられます*3.
ここで,Jacobianを計算すると $\mathrm{d}\vec{x}_{i}\mathrm{d}\vec{v}_{i}=\mathrm{d}\vec{x}_{i}\mathrm{d}\vec{v}^{\prime}_{i}$ が分かりますので,
この系の分配関数 $Z$ は,
\begin{align*}
Z & = \int\dots\int \exp\left(-\frac{H}{k_{\mathrm{B}} T}\right)\mathrm{d}^{N}\vec{x}_{i}\mathrm{d}^{N}\vec{v}_{i} \\
& = \prod_{i=1}^{N} \iint \exp\left(-\frac{1}{k_{\mathrm{B}} T} \frac{m_{i}}{2}\left(\vec{v}^{\prime}_{i}\cdot\vec{v}^{\prime}_{i}\right)\right)
\exp\left(-\frac{q_{i}\phi}{k_{\mathrm{B}} T}\right)
\mathrm{d}\vec{x}_{i}\mathrm{d}\vec{v}^{\prime}_{i} \\
& = \left(2\pi m_{i}k_{\mathrm{B}} T\right)^{\frac{3}{2}N} \prod_{i=1}^{N} \int \exp\left(-\frac{q_{i}\phi}{k_{\mathrm{B}} T}\right) \mathrm{d}\vec{x}_{i}
\end{align*}
のように計算できます*4.
残った積分に注目しましょう.
$q_{i}\phi=0$ であればこの積分は系の体積となり,最終的に理想気体の状態方程式(およびエネルギー等分配則)を導けます*5.
あるいは $\phi$ が空間的に一定の場合には被積分関数の指数を積分の外に出せて分配関数が定数倍されるだけですので,
結局理想気体の状態方程式を得ることができます.
また,スカラーポテンシャル $\phi$ のゲージ自由度を考慮すると,$\phi$ が時間的に一定である,
すなわち電場が静的(静電場)であれば,分配関数中の $\phi$ の項が無視できます.
この考察を等方性仮定の観点からまとめると,
スカラーポテンシャル(静電ポテンシャル)の変化が緩やか,すなわち電場が十分小さいか静電場であれば,
電場による荷電プラズマ粒子のエネルギー変化の速さは十分緩やかであり,衝突による粒子の熱化が支配的となります.
逆に言えば,衝突による粒子の熱化よりも速く運動の様子を変化させるほど電場が強い場合には等方性の仮定が不適となります.
*3 数式中の文字がややこしくなるので, 一般化座標 $\vec{q}_{i} $と一般化運動量 $\vec{p}_{i}$ ではなく座標 $\vec{x}_{i}$ と速度 $\vec{v}_{i}$ の関数としました. また,理想気体を考えていますので,Coulomb相互作用をはじめとする粒子間相互作用は無視しています.
*4 より厳密なプラズマ系を表現するならば化学ポテンシャルを導入して粒子数の増減を記述できる大分配関数を用いるべきなのですが, 系内の粒子数変化についてはこの項の考察の本質とは異なりますので簡単のために分配関数を計算しました.
*5 本コラムではその計算は行いませんが,統計力学の参考書を読めば必ず計算していると思います.
第5回まとめ
第5回では,プラズマが準熱平衡状態であることを実現するための条件である熱化の速度に着目した考察を行いました. プラズマの準熱平衡近似は,流体方程式中の余分な未知数である応力と熱流束を決定するための代表的な近似モデルです. 次回は,他の近似モデルである「等温過程モデル」と「断熱過程モデル」について紹介します.
ウェーブフロントでは「粒子法」でプラズマをモデル化したシミュレーションソフトウェア『Particle-PLUS』や 「流体法」のプラズマシミュレーションソフトウェア『VizGlow』を取り扱っており, これらを適宜使い分けながら皆様方へ長年ソリューションを提供しております. 本コラムを読んでプラズマシミュレーションに少しでも興味をお持ちになりましたら 資料請求や 無料セミナーなど承りますので, いつでもお気軽にお問い合わせください.
 |
上野 崚一郎 | 博士(理学) 1991年 広島県生まれ 2019年 ウェーブフロント入社 2019年 広島大学大学院理学研究科 博士後期課程修了 学生時代は数値シミュレーションを使った素粒子論(格子ゲージ理論)の研究に従事. 入社後は,専門職(エンジニア)として希薄気体解析・プラズマ解析ソフトウェアの開発をはじめとして, 解析コンサルティング業務や国内外のユーザー向けの技術サポート・トレーニングなどを担当. 最後までお読みいただきありがとうございます. お気づきの点や扱ってほしい話題がございましたらお気軽にお問い合わせください. |
