Particle-PLUS コラム - プラズマモデリング(連載) - 第3回
ウェーブフロントでは「粒子法」でプラズマをモデル化したシミュレーションソフトウェア『Particle-PLUS』や 「流体法」のプラズマシミュレーションソフトウェア『VizGlow』を取り扱っており, これらを適宜使い分けながら皆様方へ長年ソリューションを提供しております. 本コラムを読んでプラズマシミュレーションに少しでも興味をお持ちになりましたら 資料請求や 無料セミナーなど承りますので, いつでもお気軽にお問い合わせください.
第2回では, プラズマの流体モデルで使用する諸量の定義を与えました. また,Boltzmann方程式の0次モーメントを計算して連続方程式を導きました. 今回は引き続き,1次モーメントから運動量方程式を,2次モーメントからエネルギー方程式を導きましょう. (途中の式変形に興味がなければ「1.7. 流体方程式まとめ」まで読み飛ばしてください.)
1.5. 運動量方程式(運動量保存則)Momentum equation (momentum conservation)
Boltzmann方程式の1次の速度モーメントは運動量方程式を与えます.
\begin{align*}
\int m_{s}\vec{v} \left\{\frac{\partial f_{s}}{\partial t} + \vec{v}\cdot\left(\frac{\partial f_{s}}{\partial\vec{x}}\right)
+ \frac{q_{s}}{m_{s}}\left(\vec{E}+\vec{v}\times\vec{B}\right)\cdot\left(\frac{\partial f_{s}}{\partial\vec{v}}\right) \right\} \mathrm{d}\vec{v}
= \int m_{s}\vec{v} \left(\frac{\delta f_{s}}{\delta t}\right)_{C} \mathrm{d}\vec{v}
\end{align*}
[左辺第1項]
\begin{align*}
\int m_{s}\vec{v}\left(\frac{\partial f_{s}}{\partial t}\right) \mathrm{d}\vec{v}
= m_{s}\frac{\partial}{\partial t}\int \vec{v}f_{s} \mathrm{d}\vec{v}
= m_{s}\frac{\partial}{\partial t}\left(n_{s}\vec{u}_{s}\right)
= \frac{\partial}{\partial t}\left(\rho_{s}\vec{u}_{s}\right)
\end{align*}
[左辺第2項]
\begin{alignat*}{2}
\int m_{s}\vec{v} \left\{ \vec{v}\cdot\left(\frac{\partial f_{s}}{\partial\vec{x}}\right) \right\} \mathrm{d}\vec{v}
& = \frac{\partial}{\partial\vec{x}} \cdot \int m_{s}\left(\vec{v}\otimes\vec{v}\right)f_{s} \mathrm{d}\vec{v}
&& \text{ (下記参照)} \\
& = \frac{\partial}{\partial\vec{x}} \cdot \left( m_{s}n_{s}\langle\vec{v}\otimes\vec{v}\rangle \right) && \\
& = \frac{\partial}{\partial\vec{x}} \cdot \left\{ {\bf{P}}_{s} + \rho_{s}\left(\vec{u}_{s}\otimes\vec{u}_{s}\right) \right\} &&
\end{alignat*}
$\vec{v}=(v_{1},v_{2},v_{3})$,$(\partial /\partial\vec{x})=(\partial_{1},\partial_{2},\partial_{3})$ と書くと,
\begin{align*}
\text{$i$ 成分: }
\left(\vec{v}\left\{\vec{v}\cdot\frac{\partial f_{s}}{\partial\vec{x}}\right\}\right)_{i}
=v_{i}\sum_{j=1}^{3}v_{j}(\partial_{j}f_{s})
=\sum_{j=1}^{3}(v_{i}v_{j})(\partial_{j}f_{s})
=\sum_{j=1}^{3}\partial_{j}\left\{(v_{i}v_{j})f_{s}\right\}
=\left(\frac{\partial}{\partial\vec{x}}\cdot\left\{\left(\vec{v}\otimes\vec{v}\right)f_{s}\right\}\right)_{i}
\end{align*}
です.
[左辺第3,4項]
\begin{alignat*}{2}
\int m_{s}\vec{v} \left\{ \frac{q_{s}}{m_{s}}
\left(\vec{E}+\vec{v}\times\vec{B}\right)\cdot\left(\frac{\partial f_{s}}{\partial\vec{v}}\right) \right\} \mathrm{d}\vec{v}
& = q_{s}\underset{
\text{連続方程式のときと同様に $|\vec{v}|\to\infty$ で $0$}}{
\underline{
\int \frac{\partial}{\partial\vec{v}}\cdot\left\{ \left(\vec{E}+\vec{v}\times\vec{B}\right)\otimes\vec{v}f_{s} \right\} \mathrm{d}\vec{v}
}} - q_{s} \int \left(\vec{E}+\vec{v}\times\vec{B}\right) f_{s} \mathrm{d}\vec{v}
&& \text{ (部分積分/下記参照)} \\
& = - q_{s}n_{s} \left(\vec{E}+\vec{u}_{s}\times\vec{B}\right)
\end{alignat*}
$\vec{v}=(v_{1},v_{2},v_{3})$,
$\vec{E}+\vec{v}\times\vec{B}=\vec{F}=(F_{1},F_{2},F_{3})$,
$(\partial /\partial\vec{v})=(\partial_{v_{1}},\partial_{v_{2}},\partial_{v_{3}})$ と書くと,
Leibniz則は,
\begin{align*}
\text{$i$成分: }
\left(\frac{\partial}{\partial\vec{v}}\left\{\left(\vec{F}\otimes\vec{v}\right)f_{s}\right\}\right)_{i}
& = \sum_{j=1}^{3}\partial_{v_{j}}\left\{ \left( F_{j}v_{i} \right) f_{s} \right\}
\\ & = \sum_{j=1}^{3}\left[ \left( \partial_{v_{j}}F_{j} \right) v_{i}f_{s }
+ F_{j} \left( \partial_{v_{j}}v_{i} \right) f_{s}
+ F_{j} \left\{ v_{i} \left( \partial_{v_{j}}f_{s} \right) \right\} \right]
\\ & = \bigg( \underset{\text{速度発散は明らかに $0$}}
{\underline{\left( \frac{\partial}{\partial\vec{v}}\cdot\vec{F} \right)}} \vec{v}f_{s}
+ \vec{F}\cdot \underset{\text{恒等テンソル}}
{\underline{\left( \frac{\partial}{\partial\vec{v}}\otimes\vec{v} \right)}}f_{s}
+ \vec{v} \left( \vec{F}\cdot\frac{\partial f_{s}}{\partial\vec{v}} \right) \bigg)_{i}
\\ & = \left( \vec{F}f_{s} + \vec{v}\left(\vec{F}\cdot\frac{\partial f_{s}}{\partial \vec{v}}\right) \right)_{i}
\end{align*}
とできます.
[右辺]
\begin{align*}
\int m_{s}\vec{v}\left(\frac{\delta f_{s}}{\delta t}\right)_{C} \mathrm{d}\vec{v}
= \vec{K}_{s},\qquad \vec{K}_{s} = \sum_{s^{\prime}\neq s}{\vec{\mathcal{K}}}_{ss^{\prime}}
\end{align*}
${\vec{\mathcal{K}}}_{ss^{\prime}}$ は粒子群 $s$ と粒子種 $s^{\prime}$ の間の運動量交換を表します*1.
運動量保存則より,運動量交換項は ${\vec{\mathcal{K}}}_{ss^{\prime}}=-{\vec{\mathcal{K}}}_{s^{\prime}s}$ でなければなりません.
これより,明らかに ${\vec{\mathcal{K}}}_{ss}=0$ です.
*1 本コラム中では,粒子群 $s$ と$s^{\prime}$ の間の相対的ないし相互作用的な量であることを明示するための字体としてしばしばカリグラフィを用いることにます.
1.6. エネルギー方程式(エネルギー保存則)Energy equation (energy conservation)
Boltzmann方程式の2次の速度モーメントはエネルギー方程式を与えます.
\begin{align*}
\int \frac{1}{2}m_{s}\left(\vec{v}\cdot\vec{v}\right) \left\{\frac{\partial f_{s}}{\partial t}
+ \vec{v}\cdot\left(\frac{\partial f_{s}}{\partial\vec{x}}\right)
+ \frac{q_{s}}{m_{s}}\left(\vec{E}+\vec{v}\times\vec{B}\right)\cdot\left(\frac{\partial f_{s}}{\partial\vec{v}}\right) \right\} \mathrm{d}\vec{v}
= \int \frac{1}{2}m_{s}\left(\vec{v}\cdot\vec{v}\right) \left(\frac{\delta f_{s}}{\delta t}\right)_{C} \mathrm{d}\vec{v}
\end{align*}
[左辺第1項]
\begin{align*}
\int \frac{1}{2}m_{s}\left(\vec{v}\cdot\vec{v}\right)\left(\frac{\partial f_{s}}{\partial t}\right) \mathrm{d}\vec{v}
& = \frac{\partial}{\partial t}\int \frac{1}{2}m_{s}\left(\vec{v}\cdot\vec{v}\right)f_{s} \mathrm{d}\vec{v} \\
& = \frac{\partial}{\partial t}\int \frac{1}{2}m_{s}\left(\vec{u}_{s}\cdot\vec{u}_{s}
+2\vec{u}_{s}\cdot\vec{w}_{s}+\vec{w}_{w}\cdot\vec{w}_{s}\right)f_{s} \mathrm{d}\vec{v} \\
& = \frac{\partial}{\partial t}\left\{\frac{1}{2}m_{s}n_{s}\left(\vec{u}_{s}\cdot\vec{u}_{s}\right)
+m_{s}n_{s}\vec{u}_{s}\cdot\langle\vec{w}_{s}\rangle +\frac{1}{2}m_{s}n_{s}\langle\vec{w}_{s}\cdot\vec{w}_{s}\rangle\right\} \\
& = \frac{\partial}{\partial t}\left( n_{s}\varepsilon_{s}+\theta_{s} \right)
\end{align*}
ここで,$\vec{w}_{s}$ の定義 $\vec{w}_{s}=\vec{v}_{s}-\vec{u}_{s}$ より,$\langle\vec{w}_{s}\rangle=\langle\vec{v}\rangle-\vec{u}_{s}=0$ を用いました.
[左辺第2項]
\begin{alignat*}{2}
\int \frac{1}{2}m_{s}\left(\vec{v}\cdot\vec{v}\right) \left\{ \vec{v}\cdot\left(\frac{\partial f_{s}}{\partial\vec{x}}\right) \right\} \mathrm{d}\vec{v}
& = \frac{\partial}{\partial\vec{x}} \cdot \int \frac{1}{2}m_{s}\left(\vec{v}\cdot\vec{v}\right)\vec{v}f_{s} \mathrm{d}\vec{v} && \\
& = \frac{\partial}{\partial\vec{x}} \cdot
\bigg\{
\underset{
=n_{s}\varepsilon_{s}\vec{u}_{w}}{
\underline{
\frac{1}{2}m_{s}\left(\vec{u}_{s}\cdot\vec{u}_{s}\right)\vec{u}_{s} \int f_{s} \mathrm{d}\vec{v}
}}
+ m_{s}\vec{u}_{s} \underset{
\text{$\langle\vec{w}_{s}\rangle=0$ より $0$}}{
\underline{
\int \left(\vec{u}_{s}\cdot\vec{w}_{s}\right) f_{s} \mathrm{d}\vec{v}
}}
+ \underset{
=\theta_{s}\vec{u}_{s}}{
\underline{
\frac{1}{2}m_{s}\vec{u}_{s} \int \left(\vec{w}_{s}\cdot\vec{w}_{s}\right) f_{s} \mathrm{d}\vec{v}
}}
\bigg.
&& \\
& \phantom{= \frac{\partial}{\partial\vec{x}} \cdot\quad}
\bigg.
+ \frac{1}{2}m_{s}\left(\vec{u}_{s}\cdot\vec{u}_{s}\right) \underset{
=\langle\vec{w}_{s}\rangle=0}{
\underline{
\int \vec{w}_{s}f_{s} \mathrm{d}\vec{v}
}}
+ \underset{
\substack{=m_{s}\vec{u}_{s}\cdot\int(\vec{w}_{s}\otimes\vec{w}_{s})f_{s}\mathrm{d}\vec{v}\\
=(\vec{u}_{s}\cdot{\bf{P}}_{s})\hfill}}{
\underline{
m_{s}\int \left(\vec{u}_{s}\cdot\vec{w}_{s}\right)\vec{w}_{s} f_{s} \mathrm{d}\vec{v}
}}
+ \underset{
=\vec{Q}_{s}}{
\underline{
\int \frac{1}{2}m_{s}\left(\vec{w}_{s}\cdot\vec{w}_{s}\right)\vec{w}_{s} f_{s} \mathrm{d}\vec{v}
}}
\bigg\}
&& \\
& = \frac{\partial}{\partial\vec{x}}\cdot\left\{ \left(n_{s}\varepsilon_{s}+\theta_{s}\right)\vec{u}_{s}
+\left(\vec{u}_{s}\cdot{\bf{P}}\right)+\vec{Q}_{s} \right\}
\end{alignat*}
[左辺第3,4項]
\begin{alignat*}{2}
\int \frac{1}{2}m_{s}\left(\vec{v}\cdot\vec{v}\right)
\frac{q_{s}}{m_{s}}\left(\vec{E}+\vec{v}\times\vec{B}\right)\cdot\left(\frac{\partial f_{s}}{\partial\vec{v}}\right) \mathrm{d}\vec{v}
& = \frac{q_{s}}{2}\int \left(\vec{v}\cdot\vec{v}\right)
\bigg[ \frac{\partial}{\partial\vec{v}}\cdot \left\{ \left(\vec{E}+\vec{v}\times\vec{B}\right)f_{s} \right\}
- \underset{
=0}{
\underline{
\left\{ \frac{\partial}{\partial\vec{v}}\cdot \left(\vec{E}+\vec{v}\times\vec{B}\right) \right\}
}}
f_{s} \bigg] \mathrm{d}\vec{v} && \\
& = \frac{q_{s}}{2}\underset{
\text{$|\vec{v}|\to\infty$ で $0$}}{
\underline{
\int \frac{\partial}{\partial\vec{v}}\cdot \left\{ \left(\vec{v}\cdot\vec{v}\right)
\left(\vec{E}+\vec{v}\times\vec{B}\right)f_{s} \right\} \mathrm{d}\vec{v}
}}
- \frac{q_{s}}{2}\int \underset{
=2\vec{v}}{
\underline{
\left\{ \frac{\partial}{\partial\vec{v}}\left(\vec{v}\cdot\vec{v}\right) \right\}
}}
\cdot \left(\vec{E}+\vec{v}\times\vec{B}\right)f_{s} \mathrm{d}\vec{v} && \\
& = - q_{s}\int \left(\vec{v} \cdot \vec{E}\right) f_{s} \mathrm{d}\vec{v}
- q_{s}\int \underset{
=0}{
\underline{
\vec{v} \cdot \left(\vec{v}\times\vec{B}\right)
}}
f_{s} \mathrm{d}\vec{v} && \\
& = -q_{s}n_{s}\left(\vec{u}_{s}\cdot\vec{E}\right)
\end{alignat*}
[右辺]
\begin{align*}
\int \frac{1}{2}m_{s}\left(\vec{v}\cdot\vec{v}\right)\left(\frac{\delta f_{s}}{\delta t}\right)_{C} \mathrm{d}\vec{v}
= H_{s}, \qquad H_{s} = \sum_{s^{\prime}\neq s}\mathcal{H}_{ss^{\prime}}
\end{align*}
$\mathcal{H}_{ss^{\prime}}$ は粒子群 $s$ と粒子種 $s^{\prime}$ の間のエネルギー交換を表します*1.
エネルギー保存則より,$\mathcal{H}_{ss^{\prime}}=-\mathcal{H}_{s^{\prime}s}$ でなければなりません.
これより,明らかに $\mathcal{H}_{ss}=0$ です.
1.7. 流体方程式まとめSummary (fluid equiations)
プラズマの運動を流体モデルで記述する場合,これらの式を連立して,以下の3つの基本変数
- 密度 $n_{s}=n_{s}(\vec{x},t)$
- 平均速度(流速) $\vec{u}_{s}=\vec{u}_{s}(\vec{x},t)$
- 熱エネルギー $\theta_{s}=\theta_{s}(\vec{x},t)$
まず,自己無撞着な電場 $\vec{E}$ と磁場 $\vec{B}$ を別途決定する必要があります. これは通常,流体方程式に加えてMaxwell方程式 \begin{align*} & \nabla\cdot\vec{E}=\frac{1}{\varepsilon}\rho, \quad \nabla\cdot\vec{B}=0, \quad \nabla\times\vec{E}=-\frac{\partial\vec{B}}{\partial t}, \quad \nabla\times\vec{B}=\mu\vec{j}+\frac{1}{c^{2}}\frac{\partial\vec{E}}{\partial t}\\ & \text{($\rho$:全電荷密度,$\vec{j}$:全電流密度,$\varepsilon$:誘電率,$\mu$:透磁率,$c$:光速)} \end{align*} を連立して解くことにより実現できます. あるいは,静電近似が可能な場合はPoisson方程式 \begin{align*} & \nabla\cdot\left(\varepsilon\nabla\phi\right)=-\rho, \quad \vec{E} = -\nabla\phi \qquad \text{($\phi$:静電ポテンシャル)} \end{align*} を用います. なお,電磁場の解法については電磁気学の領分のため本コラムでは扱いませんのでご了承ください.
次に,高次の速度モーメント量である応力 ${\bf{P}}_{s}$ と熱流束 $\vec{Q}_{s}$ を求める必要があります. 応力については,考えているプラズマ系が満たす状態方程式を仮定する, つまり応力と密度・温度との間に何らかの関係 \begin{align*} {\bf{P}}_{s}={\bf{P}}_{s}[n_{s},T_{s}] \end{align*} が成り立つと仮定することで 方程式に現れる未知量の数を減らす場合が多いです. 熱流束については,$\vec{Q}_{s}=0$ となる状況を仮定したり, 熱伝導率 $\kappa$ を用いて $\vec{Q}_{s}=\kappa\nabla T_{s}$ とすることが一般的です.
また,各種散乱項(生成項 $S_{s}$,運動量交換項 $\vec{K}_{s}$,エネルギー交換項 $H_{s}$)についてもモデル化の必要があります. 有限の散乱項の原因としては粒子間衝突と輻射および表面反応による影響が挙げられます. したがって,必要に応じて衝突モデル・輻射モデル・表面反応モデルを加えなければなりません.
以上をまとめると,流体方程式に加えて電磁場・応力と熱流束・散乱項を決めるような連立方程式を立てることにより閉じた方程式系が得られます. 流体モデルを用いたプラズマシミュレーションでは,そのような方程式を数値的に解くことでプラズマの運動を追跡しているのです.
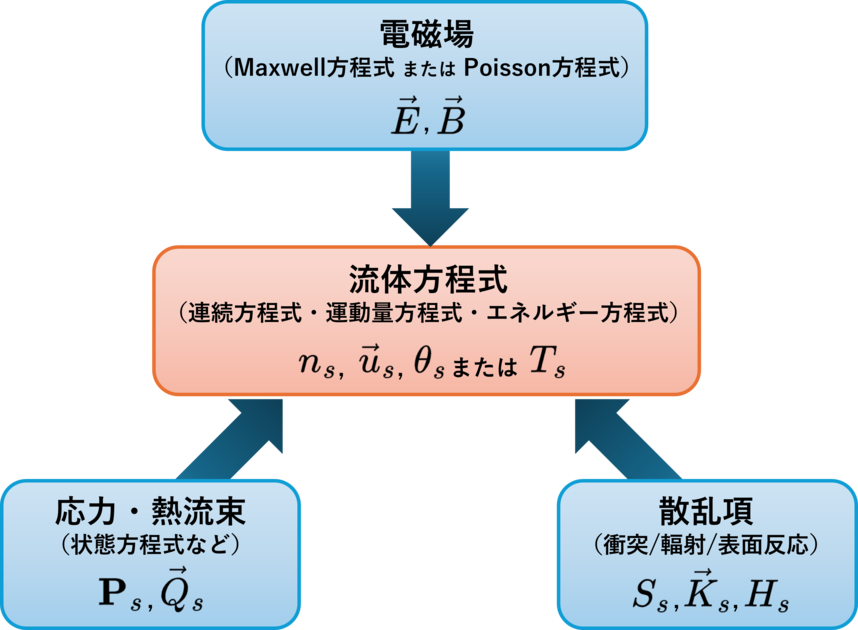
▲ 流体モデルの方程式系のイメージ図.
第3回まとめ
今回は前回に引き続き,流体モデルで実際に解かれるプラズマの流体方程式(連続方程式・運動量方程式・エネルギー方程式) の導出を完了しました. しかしながら,方程式を実際に解けるようにするためには,電磁場・応力と熱流束・散乱項に対する追加の条件が必要であることを述べました. 次回からは,その追加条件について見ていきましょう. (第4回では応力と熱流束を決めるための条件を考えます.)
ウェーブフロントでは「粒子法」でプラズマをモデル化したシミュレーションソフトウェア『Particle-PLUS』や 「流体法」のプラズマシミュレーションソフトウェア『VizGlow』を取り扱っており, これらを適宜使い分けながら皆様方へ長年ソリューションを提供しております. 本コラムを読んでプラズマシミュレーションに少しでも興味をお持ちになりましたら 資料請求や 無料セミナーなど承りますので, いつでもお気軽にお問い合わせください.
 |
上野 崚一郎 | 博士(理学) 1991年 広島県生まれ 2019年 ウェーブフロント入社 2019年 広島大学大学院理学研究科 博士後期課程修了 学生時代は数値シミュレーションを使った素粒子論(格子ゲージ理論)の研究に従事. 入社後は,専門職(エンジニア)として希薄気体解析・プラズマ解析ソフトウェアの開発をはじめとして, 解析コンサルティング業務や国内外のユーザー向けの技術サポート・トレーニングなどを担当. 最後までお読みいただきありがとうございます. お気づきの点や扱ってほしい話題がございましたらお気軽にお問い合わせください. |
