Particle-PLUS コラム - プラズマモデリング(連載) - 第1回
ウェーブフロントでは「粒子法」でプラズマをモデル化したシミュレーションソフトウェア『Particle-PLUS』や 「流体法」のプラズマシミュレーションソフトウェア『VizGlow』を取り扱っており, これらを適宜使い分けながら皆様方へ長年ソリューションを提供しております. 本コラムを読んでプラズマシミュレーションに少しでも興味をお持ちになりましたら 資料請求や 無料セミナーなど承りますので, いつでもお気軽にお問い合わせください.
1. 流体方程式Fluid Equations
プラズマを流体だと仮定してその運動を記述するときには*1,
の3つを基本変数とする場合が多いです.
これら3つの基本変数に対する3つの基礎方程式
を連立して解くことが流体モデルにおいて我々が達成するべき仕事です.
さて,これらの流体方程式はどのように導けるでしょうか.
本コラムの第1節では,流体方程式の導出を見ていきましょう.
*1 流体近似は Knudsen数 $K_{n}=\lambda/L$ がおよそ $K_{n} \ll 1$ の場合において妥当な近似です. ここで,$\lambda$ は平均自由行程,$L$ は系の代表長さです. プラズマ中では電子とイオンの平均自由行程の差が大きいので,電子についてのみ考えればOKです.
1.1. Klimontovich方程式Klimontovich equation
流体方程式の導出に向けて,まずは粒子群をEuler形式,即ち6次元位相空間中の場の量の方程式として書き下します.
粒子種が $s$ で表される粒子群を考えます.
各粒子種の6次元座標はLagrange形式で
$(\vec{\mathfrak{x}}_{\alpha}(t),\vec{\mathfrak{v}}_{\alpha}(t))$($\alpha = 1,2,\dots,N_{s}$;$N_{s}$ は粒子種 $s$ の粒子数)
と表せますので*2,
任意の座標 $(\vec{x},\vec{v})$ における粒子密度 $f_{s}$ は
\begin{align*}
f_{s}(\vec{x},\vec{v},t) = \sum_{\alpha=1}^{N_{s}} \mathfrak{f}_{\alpha}[\vec{x},\vec{v};\vec{\mathfrak{x}}_{\alpha}(t),\vec{\mathfrak{v}}_{\alpha}(t)]
= \sum_{\alpha=1}^{N_{s}} \delta[\vec{x}-\vec{\mathfrak{x}}_{\alpha}(t)] \delta[\vec{v}-\vec{\mathfrak{v}}_{\alpha}(t)]
\end{align*}
と表せます.
この $f_{s}$ の局所的な時間変化は
\begin{align*}
\frac{\partial f_{s}}{\partial t}
= \sum_{\alpha=1}^{N_{s}}
\left(\frac{\delta \mathfrak{f}_{\alpha}}{\delta \vec{\mathfrak{x}}_{\alpha}}\cdot\frac{\mathrm{d}\vec{\mathfrak{x}}_{\alpha}}{\mathrm{d}t}
+ \frac{\delta \mathfrak{f}_{\alpha}}{\delta \vec{\mathfrak{v}}_{\alpha}}\cdot\frac{\mathrm{d}\vec{\mathfrak{v}}_{\alpha}}{\mathrm{d}t} \right)
\end{align*}
です.
ここで,3次元ベクトル量 $\vec{A}=(A_{x},A_{y},A_{z})$ に関するベクトル微分演算子および
$\vec{B}=\vec{B}(\xi)$ であった場合のベクトル汎関数微分演算子として,
\begin{align*}
\frac{\partial}{\partial\vec{A}}
\equiv \left(\frac{\partial}{\partial A_{x}},\frac{\partial}{\partial A_{y}},\frac{\partial}{\partial A_{z}}\right), \quad
\frac{\delta}{\delta\vec{B}}
\equiv \left(\frac{\delta}{\delta B_{x}},\frac{\delta}{\delta B_{y}},\frac{\delta}{\delta B_{z}}\right)
\end{align*}
を導入しました.
さて,質量が $m_{s}$ で外力として
$\vec{\mathfrak{F}}_{\alpha}=\vec{F}(\vec{\mathfrak{x}}_{\alpha},\vec{\mathfrak{v}}_{\alpha},t)$ が作用している各粒子の運動方程式
\begin{align*}
\dot{\vec{\mathfrak{x}}}_{\alpha} = \vec{\mathfrak{v}}_{\alpha}, \quad
\dot{\vec{\mathfrak{v}}}_{\alpha} = \frac{\vec{\mathfrak{F}}_{\alpha}}{m_{s}}
\end{align*}
およびデルタ関数の性質
\begin{align*}
f(a)\delta(a-b) = f(b)\delta(a-b), \quad
\frac{\partial}{\partial a}\delta(a-b) = - \frac{\partial}{\partial b}\delta(a-b)
\end{align*}
を用いて,最後に式を整理すると,以下の式が得られます.
ただし,$\vec{F}_{s}=\vec{F}(\vec{x},\vec{v},t)$ としました. ちなみに,この時点での粒子密度 $f_{s}$ はデルタ関数により局所的に定義されていて, 粒子群は準中性ないし弱電離プラズマとは限らない一般のものであることに注意してください.
*2 この節に限り,粒子群ではなく個別の粒子を記述する量であることを明示するための字体としてフラクトゥールを用います. 通常の字体(イタリック)との対応は, $x\leftrightarrow\mathfrak{x}$,$v\leftrightarrow\mathfrak{v}$, $f\leftrightarrow\mathfrak{f}$,$F\leftrightarrow\mathfrak{F}$,です.
1.2. Boltzmann方程式とVlasov方程式Boltzmann equation and Vlasov equation
1.2.1. 導出
Klimontovich方程式(\ref{eq_klimontovich})を微小空間・微小時間に区切って平均化(粗視化)することで,
プラズマを粒子群として扱う際の運動論方程式を導きましょう.
今,物理量 $O$ に対して
\begin{align*}
O = \langle O\rangle + O^{\prime}
\end{align*}
となるような平均化操作 $\langle O\rangle$ を考えます.
ここで,$O^{\prime}$ は,プラズマの微視的な不安定性に起因する揺動量です.
式(\ref{eq_klimontovich})の左辺に対して平均化操作を行うと,
\begin{align*}
\langle\text{LHS of eq. (\ref{eq_klimontovich})}\rangle & =
\frac{\partial\langle f_{s}\rangle}{\partial t} + \vec{v}\cdot\left(\frac{\partial\langle f_{s}\rangle}{\partial\vec{x}}\right)
+ \left\langle\frac{\vec{F}_{s}}{m_{s}}\cdot\left(\frac{\partial f_{s}}{\partial\vec{v}}\right)\right\rangle \\
& =
\frac{\partial\langle f_{s}\rangle}{\partial t} + \vec{v}\cdot\left(\frac{\partial\langle f_{s}\rangle}{\partial\vec{x}}\right)
+ \frac{\langle\vec{F}_{s}\rangle}{m_{s}}\cdot\left(\frac{\partial\langle f_{s}\rangle}{\partial\vec{v}}\right) + C
\end{align*}
となります.
ここで,$C$ は $C=\langle uv\rangle-\langle u\rangle\langle v\rangle$ であるような,共分散に相当する量です.
さて,上式は既に平均化した物理量に対する方程式ですので,
以下では平均化操作の記号を省略して $\langle O\rangle\to O$ としましょう.
また,共分散を
\begin{align*}
C \equiv - \left(\frac{\delta f_{s}}{\delta t}\right)_{C}
\end{align*}
と書くと,プラズマ(等の粒子群)の運動論方程式として有名なBoltzmann方程式が得られます.
また,力 $\vec{F}_{s}$ がLorentz力 $q_{s}(\vec{E}+\vec{v}\times\vec{B})$ であり, $(\delta f_{s}/\delta t)_{C}=0$ であるとき,この式はVlasov方程式と呼ばれます.

▲ Ludwig Eduard Boltzmann (1844–1906,オーストリア).
1.2.2. Boltzmann方程式の意味
Boltzmann方程式の意味は,粒子の密度分布関数 $f_{s}$ が6次元位相空間および時間に関する7個の独立変数を持った関数であることから, これを時間で全微分すれば明らかです. \begin{align*} \dot{f}_{s} = \frac{\partial f_{s}}{\partial t} + \left(\frac{\partial f_{s}}{\partial\vec{x}}\right)\cdot\dot{\vec{x}} + \left(\frac{\partial f_{s}}{\partial\vec{v}}\right)\cdot\dot{\vec{v}} = \frac{\partial f_{s}}{\partial t} + \left(\frac{\partial f_{s}}{\partial\vec{x}}\right)\cdot\vec{v} + \left(\frac{\partial f_{s}}{\partial\vec{v}}\right)\cdot\left(\frac{\vec{F}_{s}}{m_{s}}\right) \end{align*} 左辺 $\dot{f}_{s}$ は粒子に沿って動く座標系における $f_{s}$ の時間変化率であり, 6次元位相空間に拡張された対流微分(covective derivative)*3そのものです. 位相空間中の座標 $(\vec{x},\vec{v})$ 付近の微小体積要素 $\mathrm{d}\vec{x}\mathrm{d}\vec{v}$ 中に含まれる粒子は全て同じ運動をしており, 衝突に代表されるような粒子の運動を散乱する要因がなければ, 時間が $\mathrm{d} t$ だけ変化して位相空間中の異なる座標 $(\vec{x}+\mathrm{d}\vec{x},\vec{v}+\mathrm{d}\vec{v})$ 付近における 微小体積要素 $\mathrm{d}\vec{x}^{\prime}\mathrm{d}\vec{v}^{\prime}$ に移動したとしても, そこに含まれる粒子数に変化はありません. 具体的には,無散乱の場合はLiouvilleの定理により $\mathrm{d}\vec{x}^{\prime}\mathrm{d}\vec{v}^{\prime}=\mathrm{d}\vec{x}\mathrm{d}\vec{v}$ が保証されますので, $f_{s}(\vec{x}+\mathrm{d}\vec{x},\vec{v}+\mathrm{d}\vec{v},t+\mathrm{d} t)=f_{s}(\vec{x},\vec{v},t)$ です. 即ち,無衝突(無散乱)であれば $\dot{f}_{s}=0$ です. 反対に,何らかの理由に起因する散乱によって粒子数の増減 $(\delta f_{s}/\delta t)_{C}$ が有限の場合には, $\dot{f}_{s}-(\delta f_{s}/\delta t)_{C}=0$ になります.
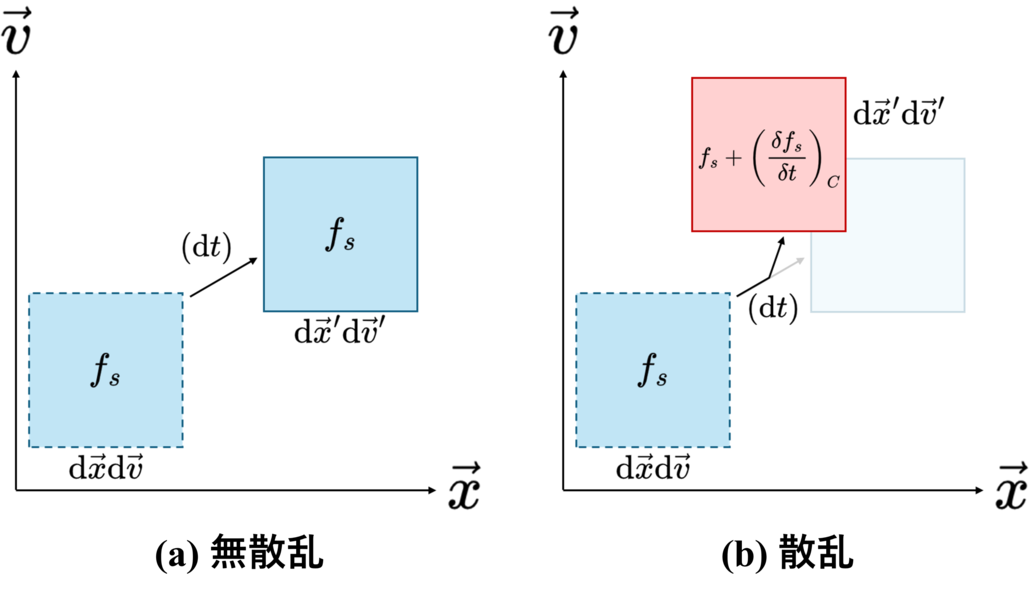
▲ 位相空間中の分布関数 $f_{s}$. 無散乱の場合は時間が変化しても対流前後で分布関数の形は変化しませんが, 散乱が起こると粒子群の運動の様子が等速直線運動の場合から外れてしまい分布関数が変化します.
*3 流体力学の言葉では実質微分やLagrange微分とも呼ばれます.
第1回まとめ
今回は,プラズマの運動論方程式としてBoltzmann方程式を導出しました. Boltzmann方程式を解けばプラズマ粒子の分布関数が得られ,それを使えば様々な現象が説明できるため非常に便利なのですが, 残念ながらBoltzmann方程式を解くのは一般的に非常に困難です. そこで,Boltzmann方程式の速度モーメントを計算することで方程式を粗視化して, モーメント量に関する方程式に書き換えることで計算を実質的に可能にするようなモデル化(=流体モデル)について 次回以降考えていきましょう.
ウェーブフロントでは「粒子法」でプラズマをモデル化したシミュレーションソフトウェア『Particle-PLUS』や 「流体法」のプラズマシミュレーションソフトウェア『VizGlow』を取り扱っており, これらを適宜使い分けながら皆様方へ長年ソリューションを提供しております. 本コラムを読んでプラズマシミュレーションに少しでも興味をお持ちになりましたら 資料請求や 無料セミナーなど承りますので, いつでもお気軽にお問い合わせください.
 |
上野 崚一郎 | 博士(理学) 1991年 広島県生まれ 2019年 ウェーブフロント入社 2019年 広島大学大学院理学研究科 博士後期課程修了 学生時代は数値シミュレーションを使った素粒子論(格子ゲージ理論)の研究に従事. 入社後は,専門職(エンジニア)として希薄気体解析・プラズマ解析ソフトウェアの開発をはじめとして, 解析コンサルティング業務や国内外のユーザー向けの技術サポート・トレーニングなどを担当. 最後までお読みいただきありがとうございます. お気づきの点や扱ってほしい話題がございましたらお気軽にお問い合わせください. |
