Particle-PLUS コラム - プラズマモデリング(連載) - 第8回
ウェーブフロントでは「粒子法」でプラズマをモデル化したシミュレーションソフトウェア『Particle-PLUS』や 「流体法」のプラズマシミュレーションソフトウェア『VizGlow』を取り扱っており, これらを適宜使い分けながら皆様方へ長年ソリューションを提供しております. 本コラムを読んでプラズマシミュレーションに少しでも興味をお持ちになりましたら 資料請求や 無料セミナーなど承りますので, いつでもお気軽にお問い合わせください.
第3章では,プラズマの流体方程式系に現れる衝突項ないし衝突の効果により運動を特徴づけるパラメータである輸送パラメータについて着目します.
第8回では,プラズマ粒子間の衝突について考察する準備としてBoltzmann方程式の右辺に現れる衝突項について一般形を求めてみましょう.
ちなみに,この章では「衝突(collision)」と「散乱(scattering)」という2つの用語をほとんど同じ意味で使っております.
(もしかすると以前の章でもそうだったかもしれませんが…)
用語の使い分けに特に意味があるわけではないので文章中で入り混じっていても気にしないでいただけますと幸いです.
物理の用語としては,「衝突」は古典粒子同士が接近して運動の様子や内部状態が変わる現象を指し,
「散乱」は衝突の結果を強調する場合や量子力学的な粒子衝突ないし波動に対して使われることが多いです.
3. 衝突と輸送パラメータCollisions and swarm parameters
前節で求めた流体方程式系を解くためには,移動度 $\mu_{s}$ や拡散係数 $D_{s}$,
散乱項 $S_{s}$, $\vec{K}_{s}$, $H_{s}$ といった輸送パラメータを決定する必要があります.
残念ながら,通常これらの輸送パラメータはガス種依存性や他の物理量(例えば,温度や換算電場)に依存するため一意に書き下すことができません.
運良く必要とする輸送パラメータに関する実験データが存在していれば,流体方程式を解く際にその値を直接参照することができますが,
それが叶わない多くの場合には何らかのモデル化を行った上で
各種輸送パラメータないし対応する衝突周波数の物理量依存性をデータテーブルとして準備しておいて,
それを参照できるようにしておく必要があります.
以上をまとめると,輸送パラメータの決定方法は以下のように大別できます.
-
輸送パラメータの実験データテーブルを準備
- これができれば話は簡単だが,考えているモデルにちょうど合致するような実験データは手に入りにくい.
-
速度分布関数を直接指定
- 衝突断面積を直接積分して衝突周波数を計算する.
- 典型的にはMaxwell分布(熱平衡)が用いられるが,低温プラズマにおける電子速度分布としての妥当性は別問題.
-
Boltzmann方程式に近似モデルを適用して求解
- この場合の輸送パラメータは,換算電場や平均エネルギーに依存する量として表される.
輸送パラメータの実験データを直接準備する以外の方法であっても, 衝突断面積や輸送パラメータの物理量依存性については実験データを必要とします. これは,散乱現象の物理は統一的な基本原理のみから説明できるものではなく,結局のところ現象論的模型の構築を必要としていることを意味しています. それであっても,考えているモデルごとに輸送パラメータの実験データを準備することに比べると, 衝突断面積や任意の近似モデル化での輸送パラメータの物理量依存性に関する実験データを準備する方がはるかに簡易なため, そのような方法がしばしば用いられます.
本章では,実験データを直接準備する方法以外の2つの方法について解説することを目標とします. まず3.1節では,Boltzmann方程式の衝突項について考えます. 次に3.2節では,衝突項の具体例として弾性散乱による運動量交換項を計算します. その後,実際に輸送パラメータを決定するための良く用いられる方法について論じます.
3.1. Boltzmann方程式の衝突項(衝突積分)Collision term/integral in boltzmann equation
プラズマ粒子を記述する運動論方程式であるBoltzmann方程式
\begin{align}
\frac{\partial f_{s}}{\partial t} + \vec{v}\cdot\left(\frac{\partial f_{s}}{\partial\vec{x}}\right)
+ \frac{\vec{F}_{s}}{m_{s}}\cdot\left(\frac{\partial f_{s}}{\partial\vec{v}}\right) = \left(\frac{\delta f_{s}}{\delta t}\right)_{C}
\label{eq_boltzmann}
\end{align}
の右辺の衝突項 $\left(\delta f_{s}/\delta t\right)_{C}$ に着目してみましょう.
ただし,衝突関して以下の状況を仮定しておきます.
- 粒子数の増減を伴うような現象として衝突による効果を独立して考えても良い*1.
- 粒子衝突は2体衝突のみである.
- 微小時間 $\mathrm{d} t$ において同じ相手と衝突するのは最大1回である.
- 微小空間 $\mathrm{d}\vec{x}\mathrm{d} \vec{v}$ 内の分布は一様である.
- 衝突前と衝突後の粒子間の相互作用は無視できる,即ち衝突に関わらない粒子種の分布関数は考えなくても良い.
- 衝突における外力の影響は無視できる.
- 衝突の時間スケールにおける分布関数の時間変化は無視できる.
これらは,プロセスプラズマを想定した低圧放電を考えるうえで妥当な近似と言えます.
さて,$\left(\delta f_{s}/\delta t\right)_{C}$ の意味するところは,分布関数 $f_{s}(\vec{x},\vec{v},t)$ の対流微分, すなわち時刻 $t$ において微小空間 $\mathrm{d}\vec{x}\mathrm{d}\vec{v}$ にあった粒子種 $s$ の粒子群の粒子密度が, 時間が $\Delta t$ だけ進んで動いた先 $\mathrm{d}\vec{x}^{\prime}\mathrm{d}\vec{v}^{\prime}$ においてどれだけ変化しているか \begin{align*} \left(\frac{\delta f_{s}}{\delta t}\right)_{C} = \lim_{\Delta t \to 0} \frac{f_{s}(\vec{x}^{\prime},\vec{v}^{\prime},t+\Delta t)\mathrm{d}\vec{x}^{\prime}\mathrm{d}\vec{v}^{\prime} - f_{s}(\vec{x},\vec{v},t)\mathrm{d}\vec{x}\mathrm{d}\vec{v}}{\Delta t} \equiv \lim_{\Delta t \to 0} \frac{\frac{N_{+}}{\mathrm{d}\vec{x}\mathrm{d}\vec{v}^{\prime}} - \frac{N_{-}}{\mathrm{d}\vec{x}\mathrm{d}\vec{v}}}{\Delta t} \end{align*} でした*2. ここで,$N_{+}$ は速度 $\vec{v}$ で運動する粒子の増加量(位置 $\vec{x}$,時刻 $t+\Delta t$ において 無衝突であれば速度 $\vec{v}^{\prime}$ であったはずの粒子数)を,$N_{-}$ はその減少量を表します. また,この粒子密度の時間変化は微小時間 $\mathrm{d} t$ の間の粒子種 $s^{\prime}$ の粒子群との衝突により引き起こされるとします.
初めに,これから考える状況についてまとめておきます.
初期時刻 $t$ において,位置 $\vec{x}$ を含む微小体積 $\mathrm{d} \vec{x}$ 中にある粒子 $s$ と $s^{\prime}$ は, それぞれ速度 $\vec{v}_{s}$ と $\vec{v}_{s^{\prime}}$ で運動しているとします. (この時点では粒子群ではなく単一の粒子を考えていることに注意してください.) ここで,衝突前の相対速度を ${\vec{v}}_{ss^{\prime}}\equiv\vec{v}_{s}-\vec{v}_{s^{\prime}}$ と書くことにします. 空間 $\mathrm{d}\vec{x}$ 中において時間が $\Delta t$ だけ進む間に粒子 $s$ と $s^{\prime}$ は衝突して, それぞれの速度は $\vec{v}_{s}^{\prime}$ と $\vec{v}_{s^{\prime}}^{\prime}$ に変化します. 衝突後の相対速度は ${\vec{v}}_{ss^{\prime}}^{\prime}\equiv\vec{v}_{s}^{\prime}-\vec{v}_{s^{\prime}}^{\prime}$ と書きます.
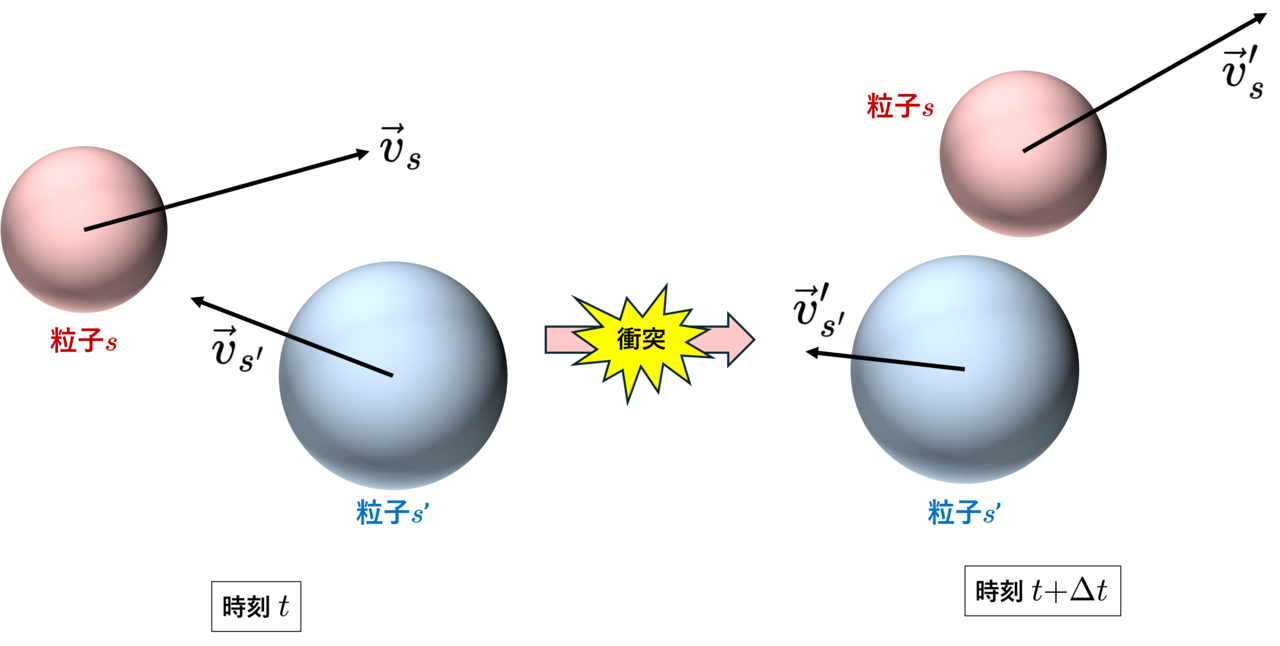
▲ 考えている衝突の状況.
ここで,入射粒子 $s$ が標的粒子 $s^{\prime}$ に衝突する際かの尺度となる物理量として衝突断面積(collision cross section)を導入します.
衝突前の微小時間直進している入射粒子 $s$ が標的粒子 $s^{\prime}$ に衝突する条件は, 2つの粒子の「何らかの方法で定義された粒子の大きさを入射粒子の直進方向に投影した影」が重なることです. この,衝突する場合に重なり得る影の総面積を衝突断面積 $\sigma_{ss^{\prime}}$ と定義します. (例えば2つの古典的な剛体球同士の接触衝突であれば,2つの剛体球の半径を $r_{1}$ および $r_{2}$ とすると, その衝突断面積は明らかに $\pi(r_{1}+r_{2})^{2}$ です.)
ここでは,標的粒子 $s^{\prime}$ を原点に固定した座標系を考えましょう. 下図に示すように,衝突パラメータ $b_{ss^{\prime}}$ で衝突した粒子の散乱角を $\theta$ としたとき, 微小にずれた位置 $b_{ss^{\prime}}+\mathrm{d} b_{ss^{\prime}}$ から入射する粒子は散乱角 $\theta+\mathrm{d}\theta$ で散乱します. 軌道を方位各方向に $\mathrm{d}\phi$ だけずらす場合と合わせて, $\theta\in[\theta,\theta+\mathrm{d}\theta]\land\phi\in[0,\mathrm{d}\phi]$ 以内の散乱を表す微小面積を 微分断面積(differential cross section) $\mathrm{d}\sigma_{ss}$ と呼び, \begin{align*} \mathrm{d}\sigma_{ss^{\prime}} = b_{ss^{\prime}} \mathrm{d} b_{ss^{\prime}} \mathrm{d} \phi = b_{ss^{\prime}} \left|\frac{\mathrm{d} b_{ss^{\prime}}}{\mathrm{d} \theta}\right| \mathrm{d} \theta \mathrm{d} \phi \end{align*} で定義します. なお,右辺の絶対値は微分断面積 $\mathrm{d}\sigma_{ss^{\prime}}$ を正値で定義するために付けました. また,各変数の範囲は $0\le \theta \le \pi$,$0\le \phi\le 2\pi$ です.
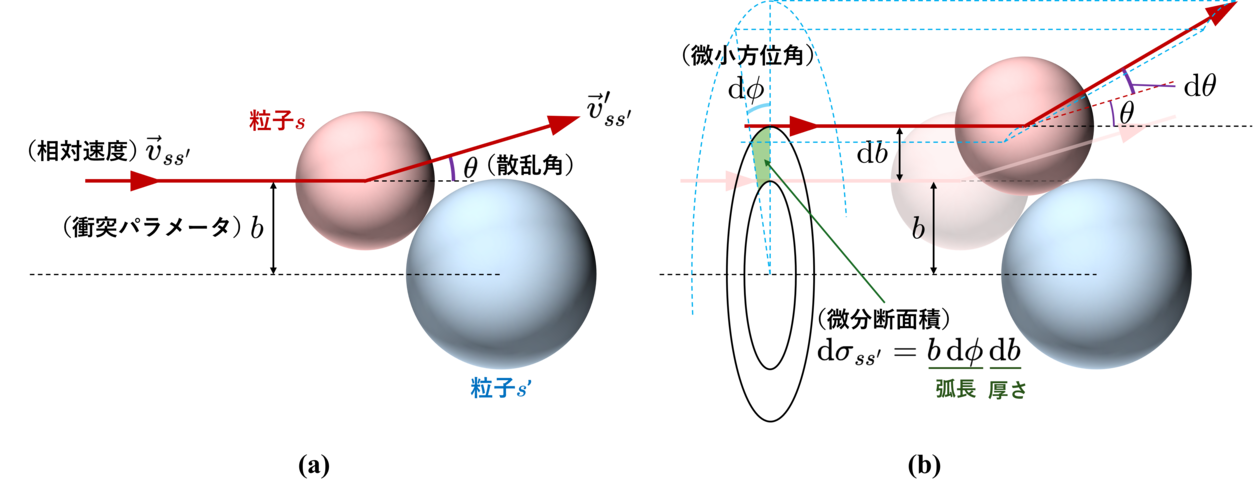
▲ 粒子 $s$ と $s^{\prime}$ の衝突散乱と微分断面積の定義. 図は剛体球同士の散乱を描いていますが,本項の内容は途中まで(次節で散乱の様子に関する仮定を導入するまで)は(擬)剛体球モデルに限らず通用します. (a) 衝突パラメータ $b_{ss^{\prime}}$ による散乱. (b) 衝突パラメータ $b_{ss^{\prime}}+\mathrm{d} b_{ss^{\prime}}$ による散乱と微分断面積 $\mathrm{d}\sigma_{ss^{\prime}}$ の定義.
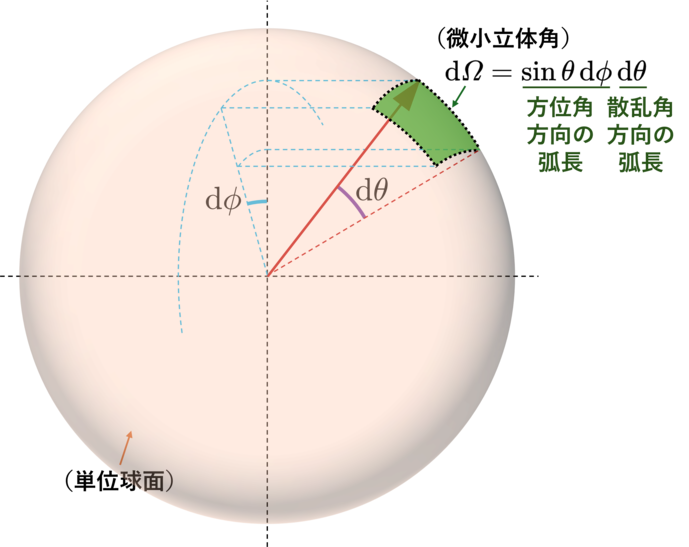
▲ 立体角の定義.
さて,粒子 $s$ は粒子 $s^{\prime}$ に向かって時間 $\Delta t$ の間に $v_{ss^{\prime}}\Delta t$ だけ接近します. したがって,時間 $\Delta t$ の間に体積 $I_{ss^{\prime}}\mathrm{d} \varOmega v_{ss^{\prime}}\Delta t$ の 円筒内に同時に存在する粒子 $s$ と粒子 $s^{\prime}$ 同士が衝突すると考えられます. (ただし,仮定より一つの粒子が $\Delta t$ の間に衝突するのは1回きりです.) 以上より,衝突する粒子 $s$ の数は \begin{align*} N_{-} = \Delta t \mathrm{d}\vec{x}\mathrm{d}\vec{v}_{s} \iint I_{ss^{\prime}}v_{ss^{\prime}} f_{s}f_{s^{\prime}} \mathrm{d}\varOmega \mathrm{d}\vec{v}_{s^{\prime}}, \quad N_{+} = \Delta t \mathrm{d}\vec{x}\mathrm{d}\vec{v}^{\prime}_{s} \iint I^{\prime}_{ss^{\prime}}v^{\prime}_{ss^{\prime}} f^{\prime}_{s}f^{\prime}_{s^{\prime}} \mathrm{d}\varOmega \mathrm{d}\vec{v}^{\prime}_{s^{\prime}} \end{align*} と表せることが分かります. また,$I _{ss^{\prime}} = I_{ss^{\prime}}(v _{ss^{\prime}},\varOmega)$, $I^{\prime}_{ss^{\prime}} = I_{ss^{\prime}}(v^{\prime}_{ss^{\prime}},\varOmega)$, $f _{i} = f_{i}(\vec{x},\vec{v}_{i},t)$, $f^{\prime}_{i} = f_{i}(\vec{x},\vec{v}^{\prime}_{i},t)$ ($i=s,s^{\prime}$)のように各物理量の引数等については略記しました.
以上より,Boltzmann方程式の右辺にある衝突項(衝突積分とも呼ばれます)の表式として以下が得られます.
*1 輻射などの効果を考える際には(衝突とは独立な現象として扱えるならば)単純に加算すれば構いません.
*2 今回導入した衝突に関するモデル化および $\left(\delta f_{s}/\delta t\right)_{C}$ の表式は, 一般にはKrook衝突項あるいはBhantnagar-Gross-Krookの単一緩和時間モデルと呼ばれるものとほとんど同義です.
第8回まとめ
第8回ではBoltzmannの衝突項(衝突積分)の一般的な表式を書き下しました. また,それに伴い衝突/散乱現象を特徴づける量として衝突/散乱断面積と微分断面積を導入しました. 次回は弾性衝突における衝突項を具体的に計算してみて,実際に運動量交換項 $\vec{K}_{s}$ を求めてみましょう.
ウェーブフロントでは「粒子法」でプラズマをモデル化したシミュレーションソフトウェア『Particle-PLUS』や 「流体法」のプラズマシミュレーションソフトウェア『VizGlow』を取り扱っており, これらを適宜使い分けながら皆様方へ長年ソリューションを提供しております. 本コラムを読んでプラズマシミュレーションに少しでも興味をお持ちになりましたら 資料請求や 無料セミナーなど承りますので, いつでもお気軽にお問い合わせください.
 |
上野 崚一郎 | 博士(理学) 1991年 広島県生まれ 2019年 ウェーブフロント入社 2019年 広島大学大学院理学研究科 博士後期課程修了 学生時代は数値シミュレーションを使った素粒子論(格子ゲージ理論)の研究に従事. 入社後は,専門職(エンジニア)として希薄気体解析・プラズマ解析ソフトウェアの開発をはじめとして, 解析コンサルティング業務や国内外のユーザー向けの技術サポート・トレーニングなどを担当. 最後までお読みいただきありがとうございます. お気づきの点や扱ってほしい話題がございましたらお気軽にお問い合わせください. |
