Particle-PLUS 事例集 - マイクロトレンチ上の薄膜生成
ウェーブフロントでは「粒子法」でプラズマをモデル化したシミュレーションソフトウェア『Particle-PLUS』や 「流体法」のプラズマシミュレーションソフトウェア『VizGlow』を取り扱っており, これらを適宜使い分けながら皆様方へ長年ソリューションを提供しております. 本コラムを読んでプラズマシミュレーションに少しでも興味をお持ちになりましたら 資料請求や 無料セミナーなど承りますので, いつでもお気軽にお問い合わせください.
計算条件Simulation Condition
Particle-PLUS では,数 $10\ \mathrm{cm}$ のチャンバ中のプラズマシミュレーションに加えて,
基板上のマイクロトレンチ(微細溝)に着目したミクロスケールの成膜シミュレーションが行えます.
今回はその一例として,溝径 $1\text{-}10\ \mu\mathrm{m}$・対径アスペクト比 $10$ のマイクロトレンチに対して
マグネトロンスパッタリングによる成膜プロセスのシミュレーションを行ってみました.
下図に示したようなマグネトロンスパッタ装置を考えます.
(マグネトロンスパッタのシミュレーションについては関連する事例集をご参照ください.)
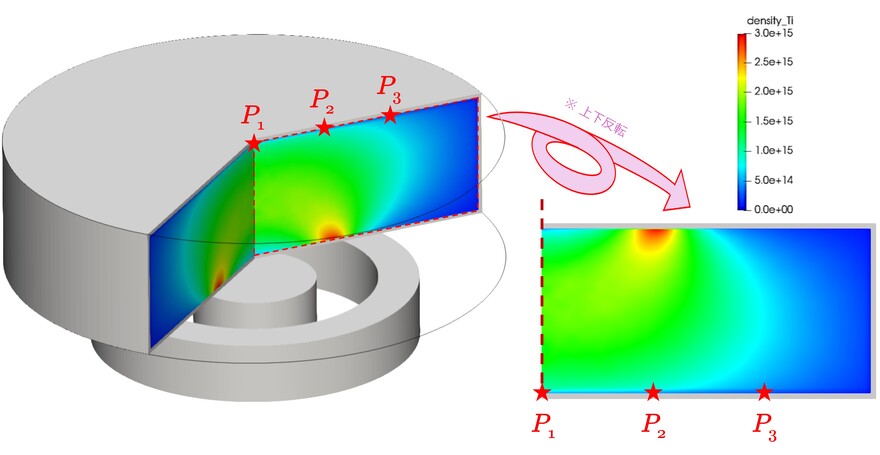
▲ アルゴンプラズマ(原料ガス $0.5\ \mathrm{Pa}$)によるマグネトロンスパッタリング(チタンターゲット)の様子. カラーマップはスパッタ粒子であるチタン原子の空間数密度 $[/\mathrm{m}^{3}]$ を示している.
さて,以下では図中に示した基板上の3点 $P_1$,$P_2$,$P_3$ におけるミクロスケールの成膜シミュレーションを行ってみましょう.
Particle-PLUS では計算モデルとして粒子法を採用していますので,基板上に入射するスパッタ粒子の速度分布を正確に評価することができます.
その結果を下図のグラフに示します.
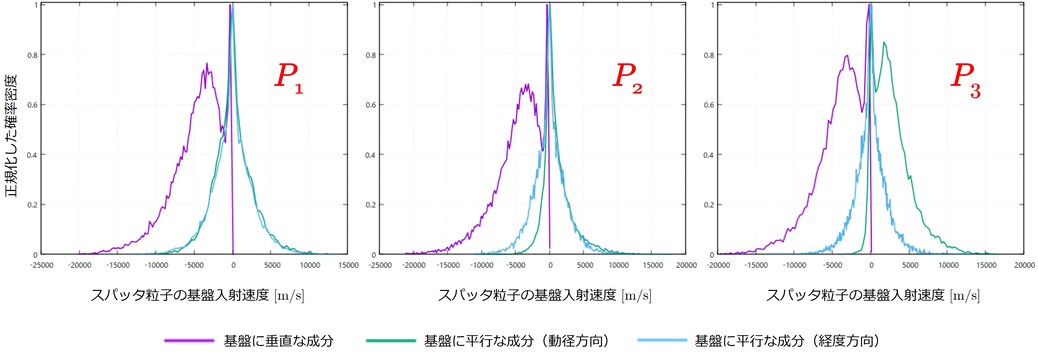
▲ 基盤に入射するスパッタ粒子の速度分布. 最頻値で正規化した確率密度としてプロットしてある. 基盤に垂直な成分(紫線)は基板からターゲットに向かう方向を正方向に, 動径方向(緑線)はチャンバ中心から側壁に向かう方向を正方向に, 経度方向(青線)は前述の2つの成分の正方向を向くベクトルの外積ベクトル方向を正方向に設定した.
基盤に垂直な速度成分(紫線)は $-4500\ \mathrm{m/s}$ 付近と $0\ \mathrm{m/s}$ 付近に2つのピークを持っています.
このうち,$-4500\ \mathrm{m/s}$ 付近のピークはスパッタ粒子の初速に依存したピークであり,
$0\ \mathrm{m/s}$ のピークはT-S間において原料ガスとの衝突により熱化されたスパッタ粒子の存在を示しています.
また,このグラフは基盤への入射粒子の速度分布ですので,当然ながら基盤に垂直な速度成分は負値のみであることに注意してください.
基盤に平行な動径方向の速度成分(緑線)については,
チャンバ中央の点 $P_1$ においては $0\ \mathrm{m/s}$ 付近にピークを持ちますが,
点 $P_2$ や $P_3$ での速度分布を見るとチャンバの外側ほどその速度成分が外側(正値側)に偏ることが分かります.
基盤に平行な経度方向の速度成分(青線)については,
この方向にスパッタ粒子が受ける力(主に原料ガスとの衝突による力積)には偏りがありませんので,
ほとんど熱平衡な分布を示すことが分かります.
以上をまとめると,チャンバ中央付近ではスパッタ粒子は基盤にほとんど垂直に入射するものの,
チャンバの外側に向かうほど入射粒子の速度成分もまたチャンバ外向きに偏ることが分かります.
また,基盤へ入射するスパッタ粒子の流束については以下のグラフが得られました.
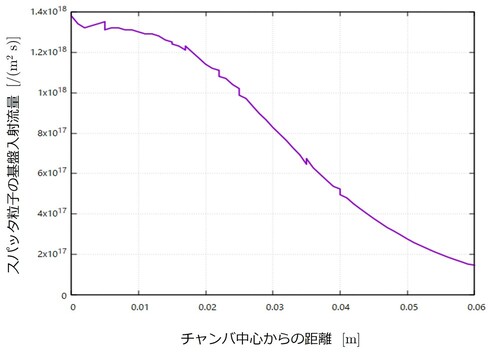
▲ 基盤に入射するスパッタ粒子の流束.
さて,ここまでに得られた基盤入射スパッタ粒子の速度分布と流束を使って,基板表面の微細構造上におけるスパッタ成膜プロセスをシミュレーションしてみましょう. 具体的には,下図で示すような計算格子(メッシュ)を用いてマイクロトレンチをモデル化します. スパッタ粒子の流入条件は上述の速度分布と流束を設定します. 背景ガス圧力は,これまでと同じくアルゴン $0.5\ \mathrm{Pa}$ です. また,トレンチのスケールによって成膜の様子に違いがあるかどうかを調べるために, 2種類の溝径($1\ \mu\mathrm{m}$ と $10\ \mu\mathrm{m}$)でシミュレーションしてみます.
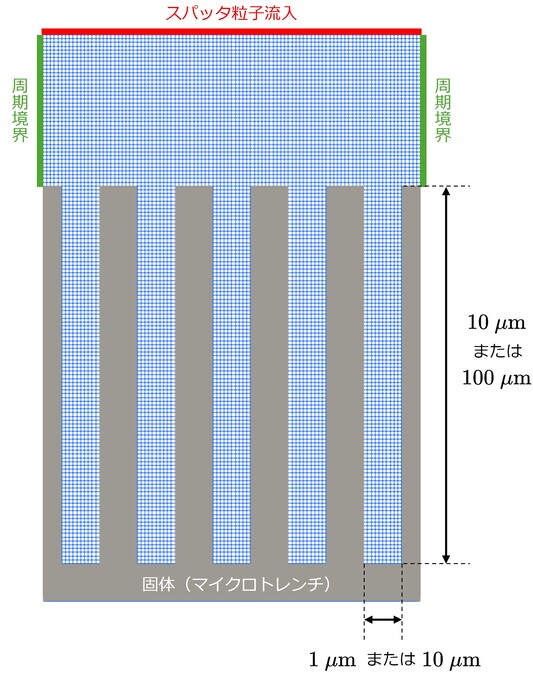
▲ マイクロトレンチシミュレーションの計算格子.
計算結果Numerical Results
マイクロトレンチシミュレーションにより得られたスパッタ粒子の空間密度分布および空間流速分布を下図に示します.
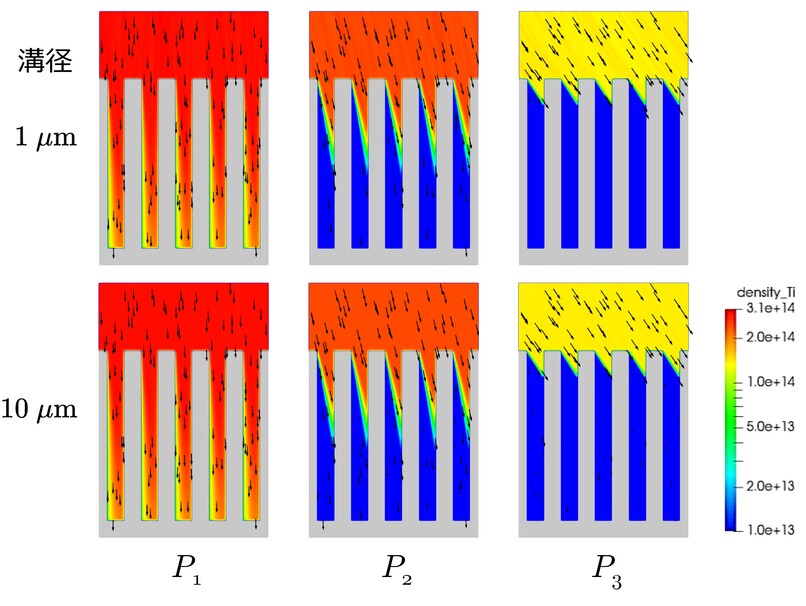
▲ マイクロトレンチに入射するスパッタ粒子の密度および流速. カラーマップが密度 $[/\mathrm{m}^{3}]$ を,矢印が流速ベクトルを表す. シミュレーションに用いた2種類の計算格子について,上段は溝径 $1\ \mu\mathrm{m}$ での計算結果を,下段は溝径 $10\ \mu\mathrm{m}$ での計算結果を示している. また,基板上の位置を示す点 $P_1$,$P_2$,$P_3$ のそれぞれでの計算結果は水平方向に並べてある.
まず,溝径による成膜の様子の違いについてはほとんど無視できると考えられます.
その理由は,アルゴン $0.5\ \mathrm{Pa}$ 中でのチタン原子の平均自由行程は概算でも $10\ \mathrm{cm}$ 程度になりますので
ミクロスケールにおいては衝突の影響が無視できるためです.
同様の理由により,トレンチのどの部分にスパッタ粒子が到達しやすいかについても
基盤(付近)へのスパッタ粒子の入射角の違い(=点 $P_1$,$P_2$,$P_3$ の違い)が直接的に影響していることが分かります.
次に,成膜速度(デポジションレート)を可視化した図を示します.
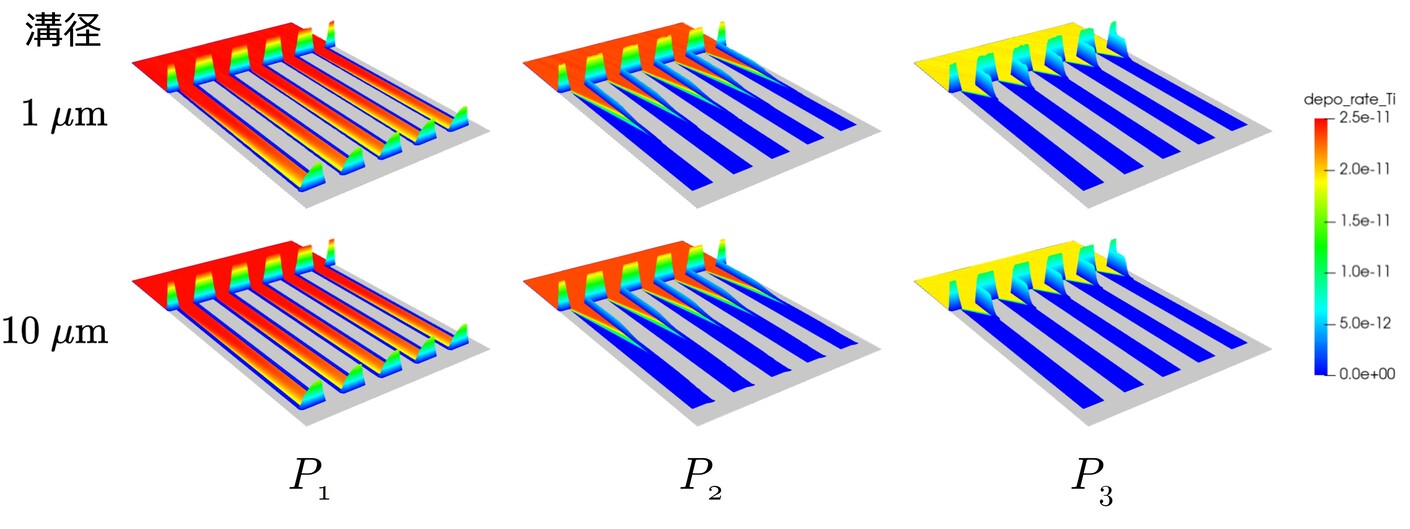
▲ マイクロトレンチ上におけるスパッタ粒子の堆積速度 $[\mathrm{m}/\mathrm{s}]$. 見やすさのために堆積速度の値で押し上げて表示してある. 底面のカラーマップは密度を表す.
先ほど議論したように,スパッタ粒子の基盤入射角による粒子が到達しやすい部位の違いがそのまま堆積速度の違いに関連付いています. チャンバ中央付近 $P_1$ においてスパッタ粒子はほとんど垂直に基盤に入射しますので, 粒子はトレンチの底まで到達して溝を埋めるように堆積していくことが分かります. 一方で,点 $P_2$ や $P_3$ ではトレンチの浅い側壁付近ばかりにスパッタ粒子が堆積しますので, プロセスが進むと最終的に基板上に微細空洞が生じることが容易に想像できます. したがって,薄膜中にそのようなエアーギャップを意図的に作成することが目的でないのでしたら, スパッタ粒子ができる限り基盤に垂直に入射するような装置設計が望ましいと考えられます.
まとめSummary
今回はマイクロトレンチ上へのスパッタ成膜プロセスについて,ミクロスケールのモデル化を行いシミュレーションしてみました.
通常マグネトロンスパッタリングの駆動圧力は $O(1)\ [\mathrm{Pa}]$ 以下ですので,
ミクロスケールのトレンチ内部やその付近では粒子衝突が起きません.
その結果として,トレンチ上のどの部位の膜厚が大きくなりやすいかなどは,
スパッタ粒子が基盤に到達する直前の入射角度から直接的な影響を受けることが分かりました.
言い換えると,薄膜の微細構造を制御するためには,磁石配置や基盤の設置角度などをマクロな視点で制御した上で,
さらに基板表面のミクロな凸凹に対して入射粒子が当たる部位と陰になる部位をミクロな視点で制御するという高度な最適化が必要なことを意味しています.
(これはマグネトロンスパッタによる成膜に限らず,もう少し高圧力帯で駆動するCVDによるトレンチ成膜でも必要な視点でしょう.)
Particle-PLUS では,マクロな条件を変化させながら行うマクロスケールのシミュレーションと
ミクロ形状を調整しながら行うミクロスケールのシミュレーションを組み合わせて行うことで,
マクロな視点とミクロな視点の両方から成膜プロセスを観察することが可能です!
ぜひとも,我々にそのような高難度の薄膜生成・装置設計業務の支援をさせていただければ幸甚です.
少しでもご興味がございましたらお気軽にお問い合わせください.
 |
上野 崚一郎 | 博士(理学) 1991年 広島県生まれ 2019年 ウェーブフロント入社 2019年 広島大学大学院理学研究科 博士後期課程修了 学生時代は数値シミュレーションを使った素粒子論(格子ゲージ理論)の研究に従事. 入社後は,専門職(エンジニア)として希薄気体解析・プラズマ解析ソフトウェアの開発をはじめとして, 解析コンサルティング業務や国内外のユーザー向けの技術サポート・トレーニングなどを担当. 最後までお読みいただきありがとうございます. お気づきの点や扱ってほしい話題がございましたらお気軽にお問い合わせください. |
