コラム - 超粒子って何？ ～ DSMC法とPIC法の基礎知識 ～

粒子法^*1 と呼ばれる計算手法の一部では 、超粒子^*2 (super particle) という概念を導入します。 弊社で取り扱っている粒子法解析ソフトウェア DSMC-Neutrals や Particle-PLUS では超粒子を用いています^*3。

この資料では、超粒子に関する以下の疑問にお答えします。

• 超粒子とは何か？
• 何のために導入するか？
• 実現象と矛盾しないのか？

1. 大雑把に言えば、計算対象(液体や気体)を小さな粒子の集合体として扱い、 各粒子に対する運動方程式を解く計算手法です。 他の代表的な計算手法としては流体法や差分法などがあります。
2. 「計算粒子」や「サンプル粒子」、「シミュレーション粒子」などとも呼ばれます。
3. DSMC-NeutralsではDSMC法(Direct Simulation Monte Carlo method) 、Particle-PLUSではPIC法(Particle In Cell method)という粒子法の計算アルゴリズムを採用しています。

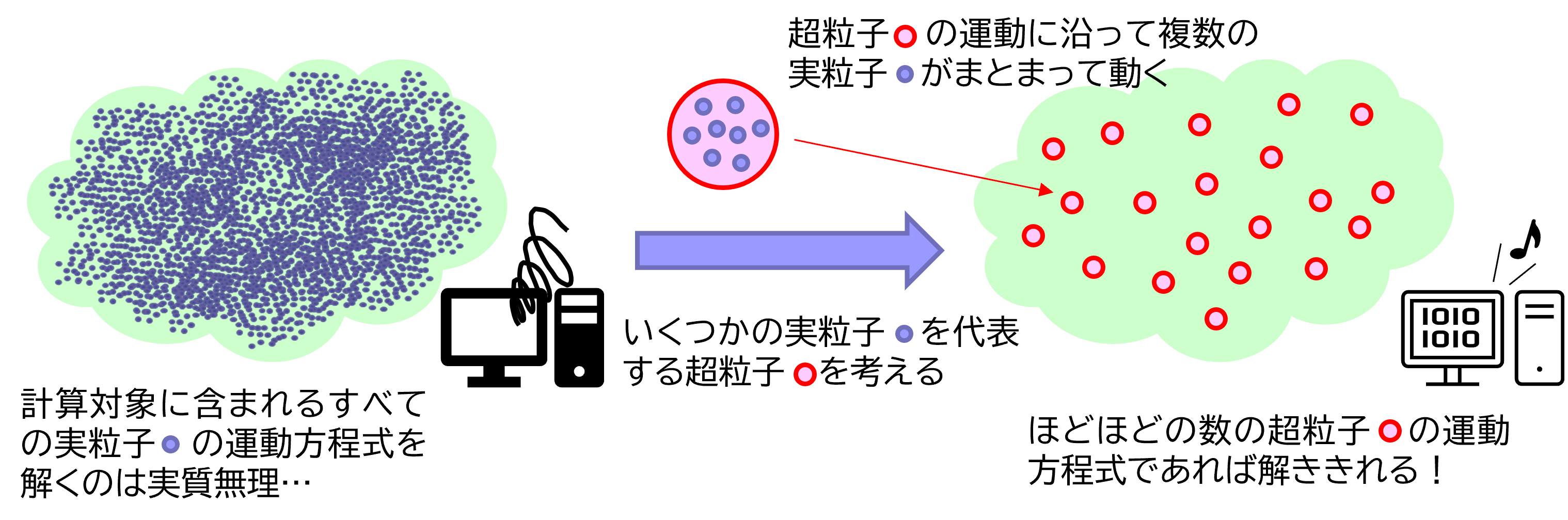
マクロな現象のシミュレーションをする際、最新のスーパーコンピュータをもってしても Avogadro数個のすべての粒子の挙動を計算することは、メモリと時間のどちらの観点からもまず不可能です。 そこで、ある程度まとまった数の粒子を代表するひとつの代表粒子を考えます。 この代表粒子を 超粒子 と呼びます。 DSMC法やPIC法など粒子法の一部では 、「超粒子の挙動は、いくつかのまとまった粒子の挙動をまとめて表している」という近似を行います。 Avogadro数よりも桁で少ない数の超粒子の挙動だけを計算することで、 現実的な計算コストでシミュレーションができるようになります。

前ページで述べたように、超粒子を使うことは統計上は近似でしかありません。 そこで、DSMC-NeutralsやParticle-PLUSでは 、すべての実粒子の運動方程式を解いた場合と矛盾しないように、 『時間的な平均値』を計算しています。

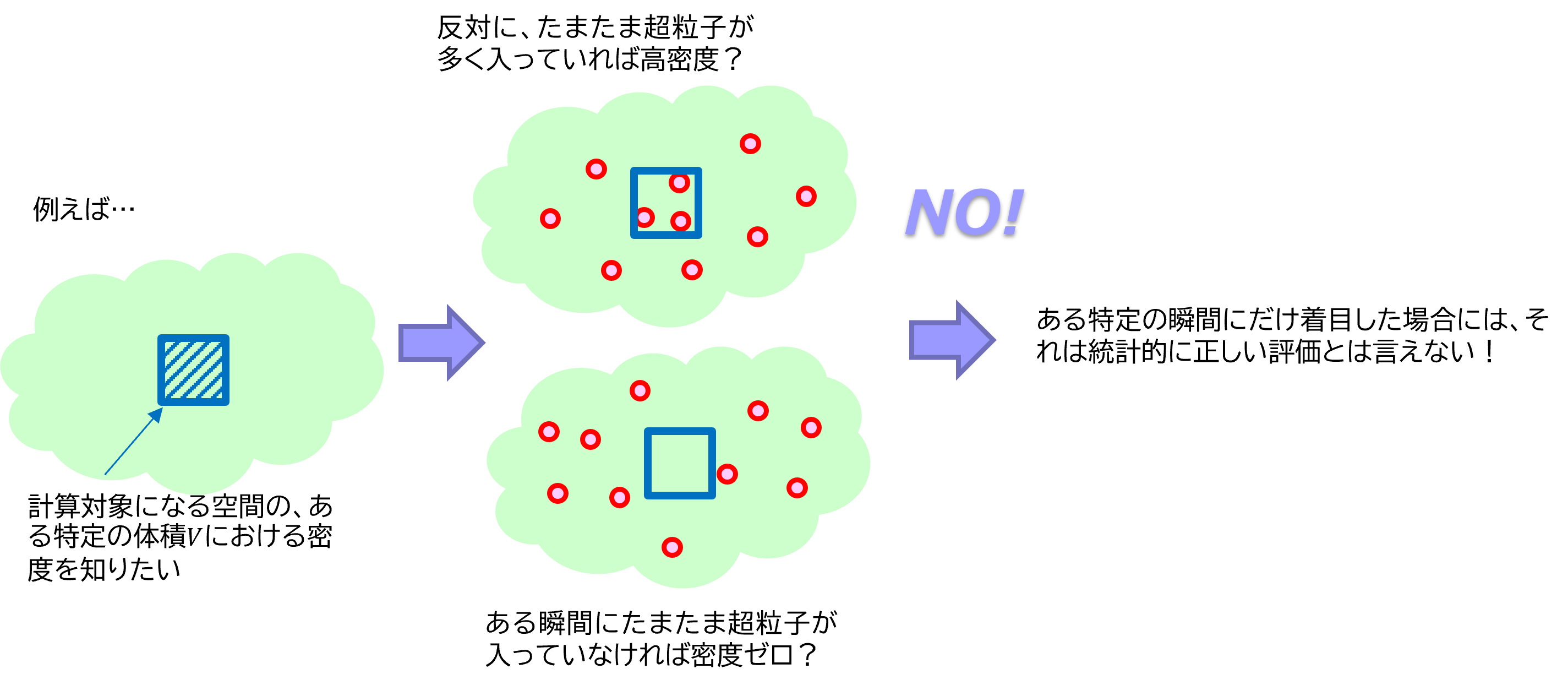
ある程度の幅のある時間 T = (T_f - T_i) 間の複数の瞬間的なスナップショットを用意します。 そうすると、時間 T の間に体積 V の中に超粒子(図中の赤丸)が平均的に何個入っていたかを求めることができます。 平均的に入っていた超粒子の数が実粒子換算で N 個 だったとすると、求めたい密度は N /V ということになります。 ちなみに、複数の瞬間的なスナップショットを用意する一連の処理を サンプリング と呼んだりします。

ある体積に含まれる超粒子がサンプリングをしてもなお少ない場合に統計的に正しい評価ができているか不安になりますが、 大抵の場合そもそもその場所に粒子はほとんどやってこないし、粒子が少なければ衝突もめったに起きないため、 シミュレーション結果に問題はありません。 （もちろん、ひとつの超粒子が代表する実粒子の数が多すぎる場合やサンプリングの時間が短すぎる場合などは別です。）

ひとつの超粒子を実粒子数に換算するといくつ分に相当するかの値のことを 超粒子の「重み（weight）」と呼びます。

\begin{align*} w = \frac{N_{\rm real}}{N_{\rm super}} \end{align*}

,

$w$ : 重み $N_{\rm real}$ : 計算領域内の実粒子数 $N_{\rm super}$ : 計算領域内の超粒子数

重みは計算の精度や負荷に関わる重要なシミュレーションパラメータです。 DSMC-NeutralsやParticle-PLUSでは、初期状態の重みを、

\begin{align*} w = \frac{nV_{\rm cell}}{N_{\rm initial}} = \frac{PV_{\rm cell}}{k_{\rm B}TN_{\rm initial}} \end{align*}

,

$n$ : 密度 ,   $P$ : 圧力 ,   $T$ : 温度 $k_{\rm B}$ : Boltzmann定数 $V_{\rm cell}$ : 計算格子の平均セル体積 $N_{\rm initial}$ : セル当たりの初期超粒子数

で決定して、その後は計算の進捗とともに重みを適切な値に自動調整する機能が備わっています。 ちなみに、重みの目安値としては、例えばPIC法だと経験的に Ο (10^5—7) くらいに調整することが多いです。

1. 参考文献
2. [H. C. Kim, et. al., 2005]