コラム - 磁気ミラー効果のシミュレーション
第4稿 2025/09/08 … 式(1)の訂正
. はじめに Intoroduction & Table of Contents
カスプ型の非一様磁場中でプラズマが閉じ込められるプロセスは, 磁気ミラー領域における荷電粒子の反射, 損失により説明される事が多い. 磁気ミラーの効果は, スパッタ装置等で利用されるマグネトロンプラズマの基本原理であり, 他には核融合炉や粒子加速器へも応用されている[参考1,2,3]. また, 地磁気圏のオーロラ研究においても重要な効果の1つである[参考4].
しかし, 今までのプロセスプラズマのシミュレーションモデルでは, 磁場だけでなく電場や衝突によっても速度分布が乱されるために, 磁気ミラー効果のみを可視化して精度良く評価する事が困難であった. 本記事では, 磁気ミラー効果の評価を目的とした計算モデルを構築し, そのシミュレーション結果と共に報告する.
 記載内容 (頁内リンク)
記載内容 (頁内リンク)
- はじめに
- シミュレーション設定
- 関連用語と変数記号
- 出力変数と評価項目
- シミュレーション結果 - 電子1つの解析
- シミュレーション結果 - 複数電子の解析
- まとめ
- 付録. 理論式の導出
- 補注
- 参考資料
. シミュレーション設定 Simulation Settings
非一様磁場中の電子の運動を, 粒子法の一種である Particle-in-Cell 法(PIC法)でシミュレーションした. ツールには弊社で開発されたソフトウェアである Particle-PLUS[参考5] を用いた. 空間は軸対称を想定してモデル化し, 2次元の計算メッシュを用いた. 磁場配置は, Particle-PLUS で使用されている基本例題(マグネトロンプラズマのチュートリアル)と同じものである. その例題のシミュレーション結果を下図に示す.
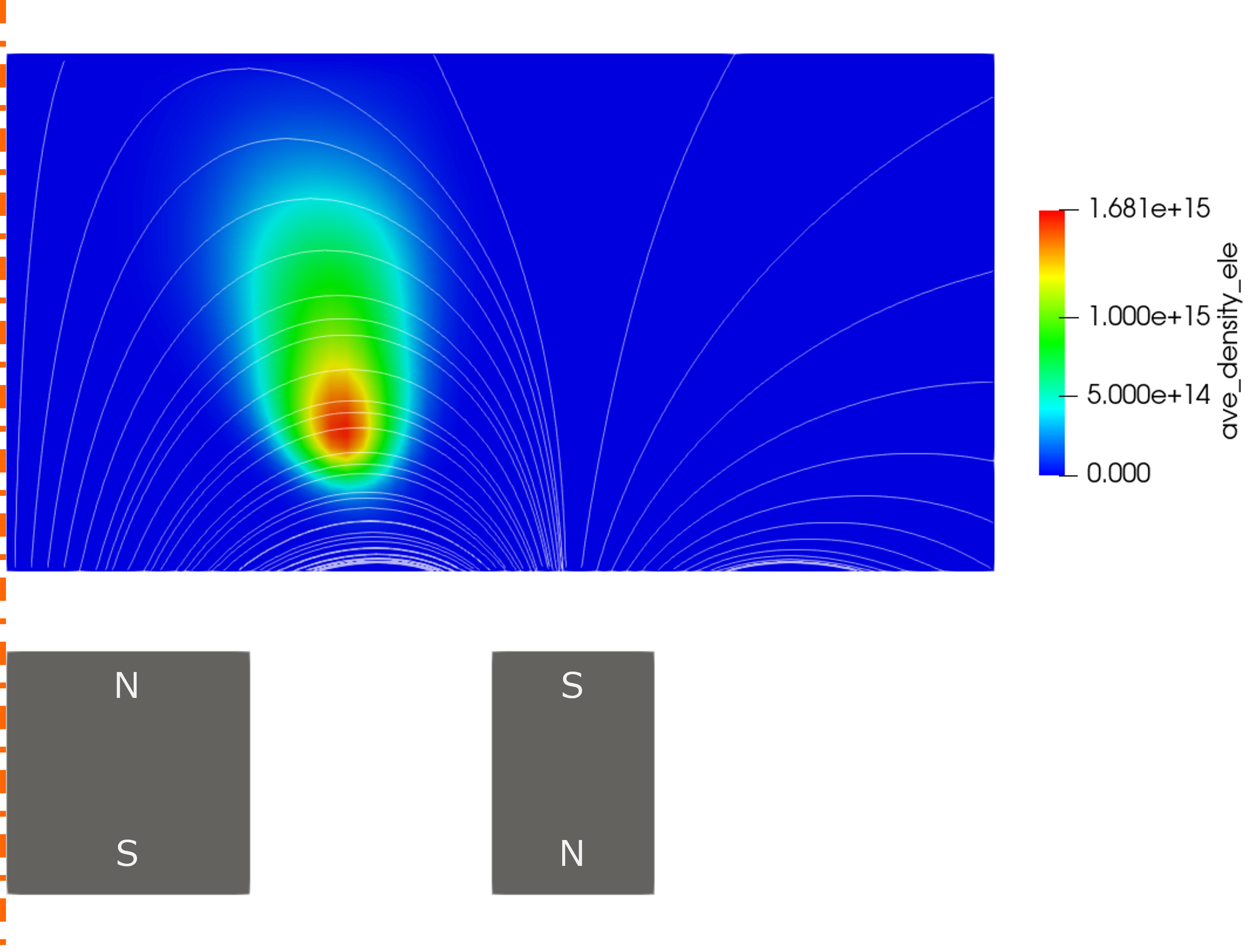
▲ 軸対称マグネトロンプラズマのシミュレーション結果
カラーマップは電子数密度, 白線は磁束密度ベクトルの流線を表している.
今回は, 図で示されているプラズマの部位に複数の電子を配置して, その後の運動の様子を観察した. 電子群の初速は温度1eVのマクスウェル分布(補注a) で与えている. なお, 電場(境界条件から与えられる電場, および空間中の荷電粒子が生成する電場)の存在は, 今回は評価の邪魔となる. その影響を無くすために, 空間全域の電位はゼロに固定している.
. 関連用語と変数記号 Related Words, Variables, and Symbols
ミラー効果は磁気モーメントの断熱不変性から説明される. 関連用語および変数の定義と, それらが持つ意味を本節にまとめておく. 各種理論式の導出過程は 付録 に記載する.
 3.1. 変数記号
3.1. 変数記号
本記事内では荷電粒子の変数について次表の記号を用いる.
▼ 変数表
矢印で表される3次元ベクトル量の大きさは, 矢印が無い場合の同じ文字を用いて表すものとする. 例えば, 磁場ベクトル $\vec{B}$ の大きさは $B$ である.
| 記号 | 意味 |
| $\vec{B}$ | 荷電粒子が受ける磁場(局所磁場)(補注b) |
| $m$ | 質量 |
| $\vec{v}$ | 速度 |
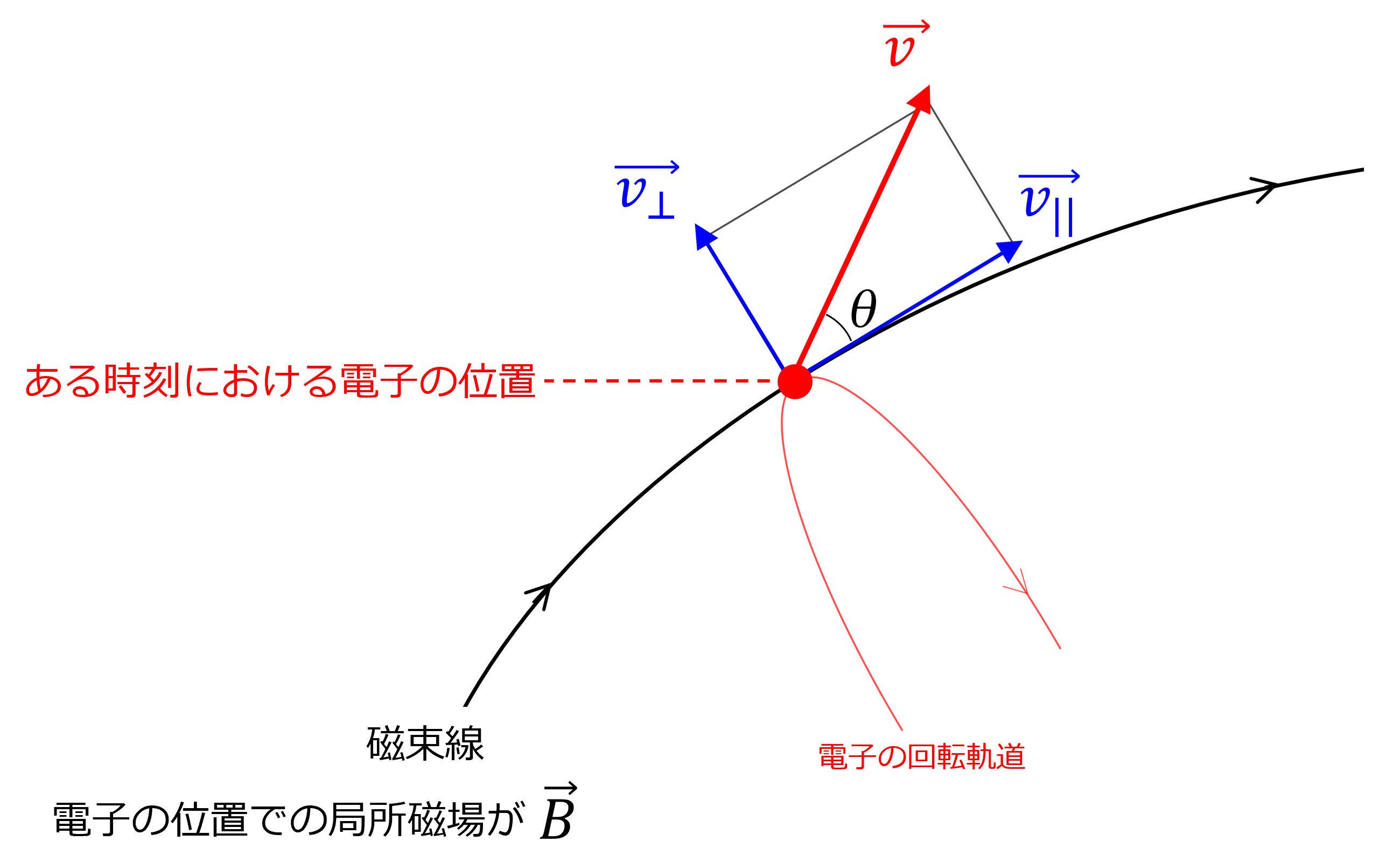
| $\vec{v}_{/\!/}$ | $\vec{v}$ のうち $\vec{B}$ に平行な成分(下図参照) |
| $\vec{v}_{\perp}$ | $\vec{v}$ のうち $\vec{B}$ に垂直な成分(下図参照) |
| $\theta$ | $\vec{B}$ に対する $\vec{v}$ のピッチ角(3.3節参照) |
| $K$ | 運動エネルギー |
| $\mu$ | 磁気モーメント(3.2節参照) |
| $R$ | ミラー比(3.3節参照) |
 \begin{align}
\vec{v}_{/\!/} &:= \frac{( \vec{v} \cdot \vec{B}) \vec{B}}{B^2} \\
\end{align}
\begin{align}
\vec{v}_{⊥} &:= \vec{v} - \vec{v}_{/\!/} \\
\end{align}
\begin{align}
\vec{v}_{/\!/} &:= \frac{( \vec{v} \cdot \vec{B}) \vec{B}}{B^2} \\
\end{align}
\begin{align}
\vec{v}_{⊥} &:= \vec{v} - \vec{v}_{/\!/} \\
\end{align}
▲ 荷電粒子の速度に対する $\vec{v}_{/\!/}$ , $\vec{v}_{\perp}$ の定義
また, 本記事では, ある磁束線に沿って運動する荷電粒子の位置と, 受ける磁場が最も弱くなる位置, 最も強くなる位置, の3種類を区別して記述する場合がある. それらの位置を表す添字として ${\rm c}$ , $0$ , $1$ を使用する. 例えば, $B$ の瞬時値を $B_{\rm c}$ , 最小値を $B_0$ , 最大値を $B_1$ のように表記する(付録図参照).
 3.2. 磁気モーメント
3.2. 磁気モーメント
磁場中でローレンツ力を受けて旋回運動(補注c) している荷電粒子の 磁気モーメント(Magnetic Moment)$\mu$ は次で定義される. \begin{align} \mu := \frac{mv_\perp^2}{2B} \end{align} これは一般的な周期系における 作用変数(Action Variable)に相当し, 周期に対して $B$ が緩やかに変化する場合は一定不変に保たれる(補注d,e). このような量を 断熱不変量(Adiabatic Invariance)という[参考1,6,7]. この不変性に着目すると, $B$ と $v_\perp$ の間には, 下図に示す関係が成り立つ.
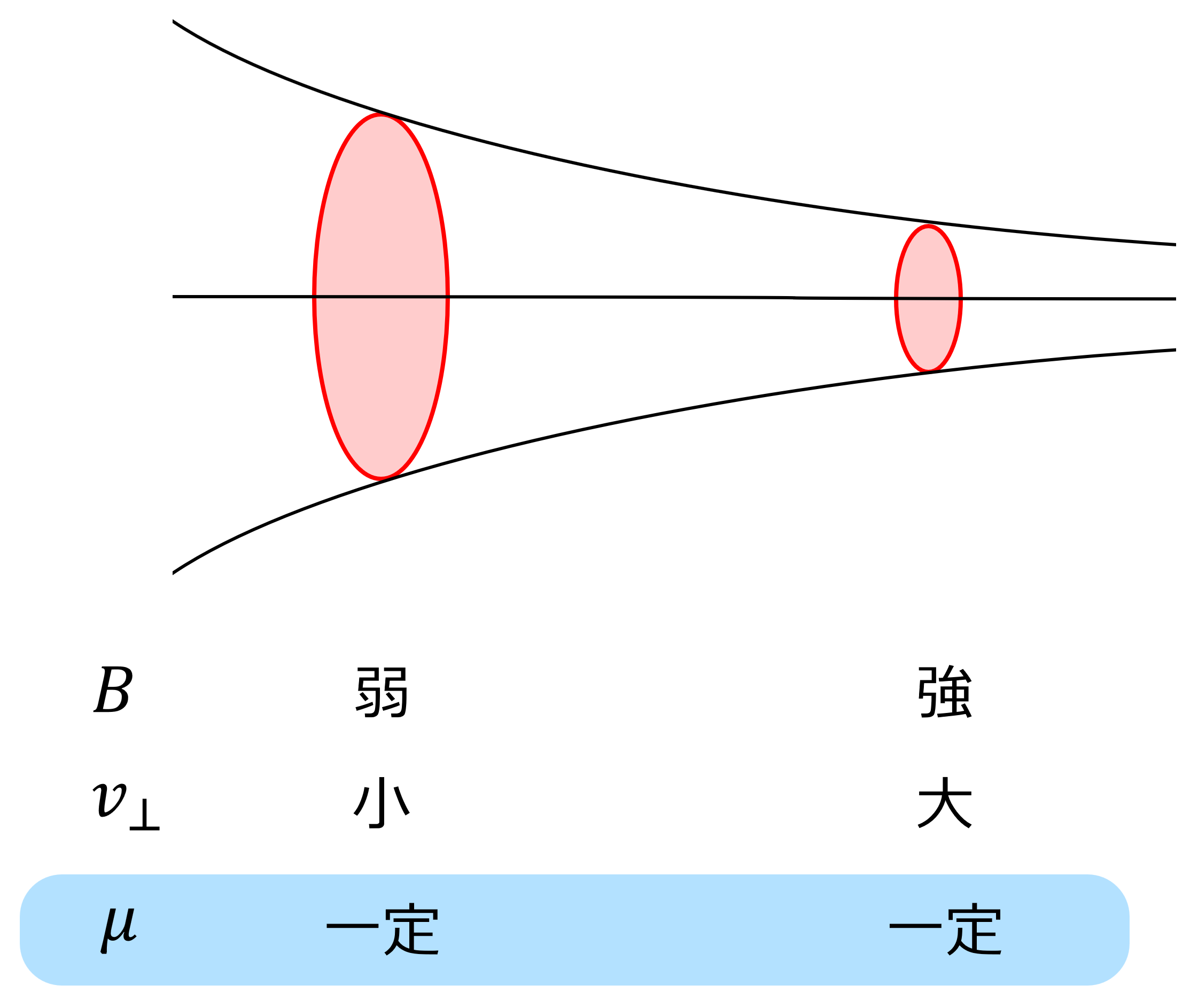
▲ 磁気モーメントの断熱不変性
 3.3. 磁気ミラー
3.3. 磁気ミラー
上図で示したような, 磁束線が漏斗状に収束している領域では $B$ が強くなる. 荷電粒子がそこに近づくと, $\mu$ を一定に保つために $v_{\perp}$ は増大するが, 全運動エネルギー $K := \frac{1}{2}mv^2$ が一定であるため, 必然的に $v_{/\!/}$ は減少することになる. そして, $B$ が十分大きい場合は $v_{/\!/} = 0$ となり, その位置で旋回中心の進行方向が反転する. この現象を ミラー効果(Mirror Effect)という.
プラズマの磁気閉じ込めでは, 2つの磁気ミラーで挟んだ磁場配位がよく利用される(下図参照). この場合, 荷電粒子の感じる磁場は真ん中で最も弱くなり, ミラー領域で最も強くなる. それらの磁場強度の比, \begin{align} R := \frac{B_1}{B_0} \quad (> 1) \end{align} を ミラー比(Mirror Ratio)という. これはミラー効果の強さを特徴付ける量であり, 粒子は理想的には反射を繰り返して $B/B_0 \le R$ の弱磁場領域に閉じ込められる(付録2参照). 十分大きなミラー比が確保されない場合, 粒子は反射されずに逃げてしまう.
ここで, $\vec{v}_{/\!/}$ と $\vec{v}$ の成す角(ピッチ角)$\theta$ を, 次式に示す形で導入する(補注f). \begin{align} \tan \theta := \frac{v_{\perp}}{v_{/\!/}} \quad (0 \le \theta \le 90°) \end{align} このとき, 閉じ込められる粒子に対しては $\mu$ と $K$ の不変性から次の関係が導かれる(付録1参照). \begin{align} R = 1/\sin ^2 \theta _0 \end{align} これは驚くべき結果であり, すなわちその荷電粒子の閉じ込めに必要なミラー比の大きさは, 質量や電荷に依らず, ピッチ角で決まるという事を意味する.
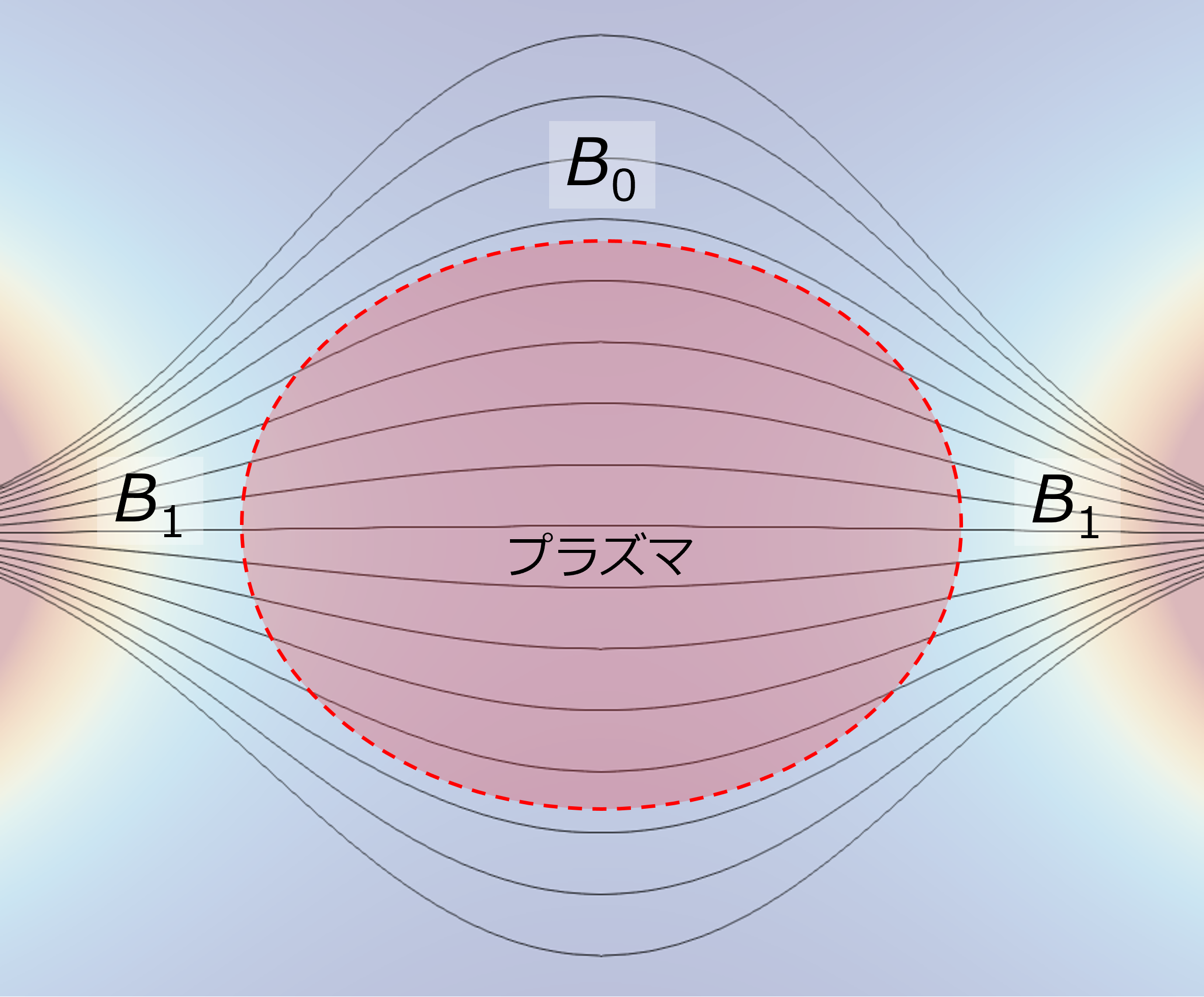
▲ 対向型磁気ミラーによるプラズマの閉じ込め(イメージ)
B0 と B1 は磁束線ごとに異なる値を取る.
 3.4. ロスコーン
3.4. ロスコーン
$\theta$ の小さい粒子は $v_{/\!/} = 0$ となる事ができず, ミラー領域を通過して逃げ出す(付録3参照). ミラー領域から粒子が失われる現象を ミラー損失(Mirror Loss)という. この範囲は速度空間では下図のように円錐状となっており ロスコーン(Loss Cone; 損失円錐)と呼ばれる. このときの荷電粒子の速度分布関数は $\theta/\theta _0 \lt 1$ の円錐部分が損失した非等方分布になり, 結果としてマクスウェル-ボルツマン分布からずれる[参考6].
今回は扱わないが, もし衝突等によりピッチ角が変化してロスコーン内へ散乱されると, その粒子は失われる. 一般に, 電子はイオンに比べて高い衝突周波数を持つため, より容易に失われる[参考1].
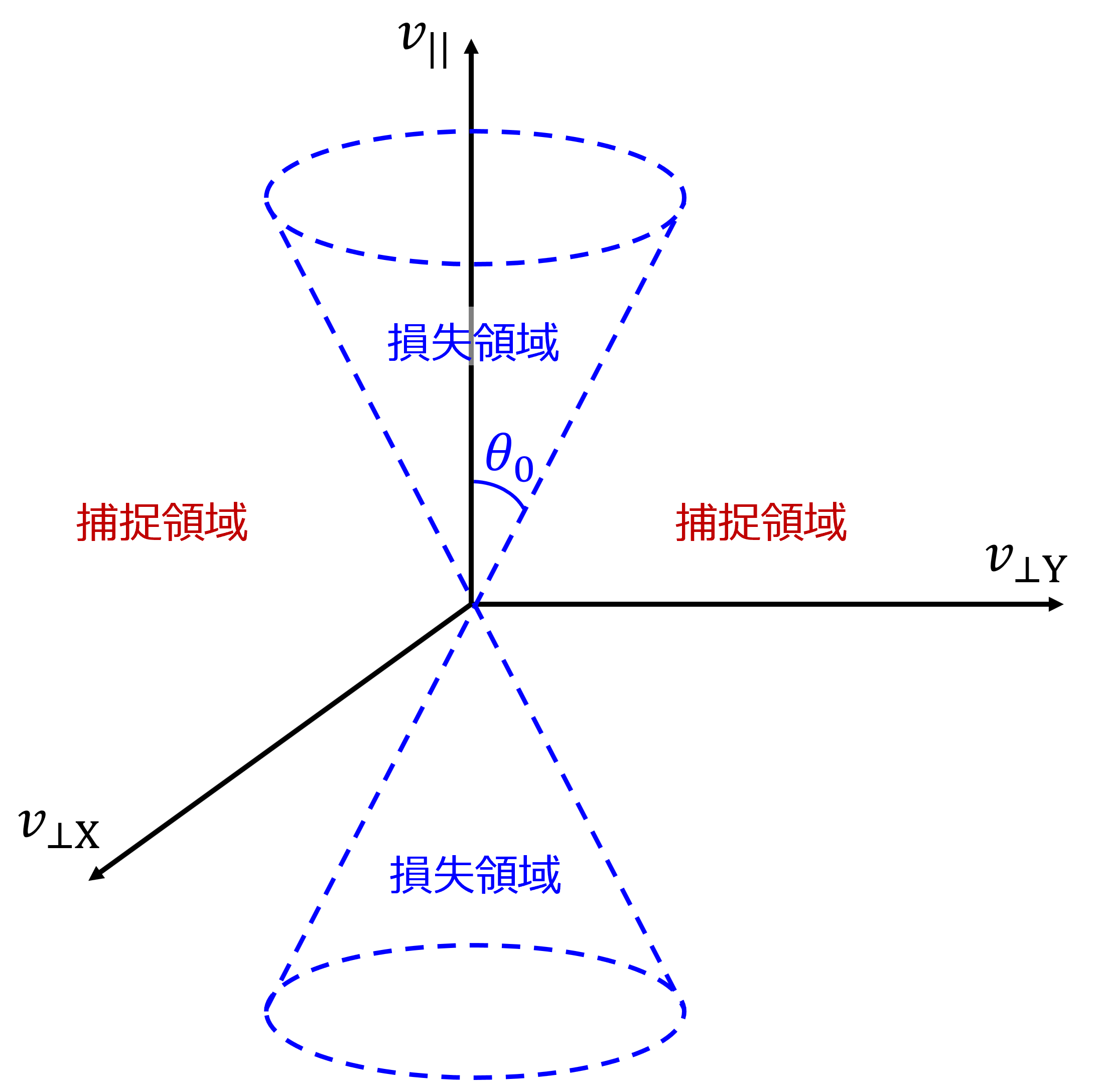
▲ 荷電粒子の捕捉領域と損失領域(ロスコーン)
この図は教科書等に倣って3次元速度空間を描画している. $v_{\perp}$ の添字2つは便宜上付けられているだけであり, 位置座標 X, Y とは無関係である. 方位角に関する対称性のため, $v_{\perp {\rm X}}$ 軸と $v_{\perp {\rm Y}}$ 軸の方向の取り方に関しては任意性がある (${v_{\perp}}^2 = {v_{\perp {\rm X}}}^2 + {v_{\perp {\rm Y}}}^2$) . また天頂角に関しても θ=90° を境界として鏡面対称のため, 結局のところ, ロスコーンは $v_{/\!/}$ と $v_{\perp}$ の2軸から成る座標平面の第1象限内で図示すれば十分である.
. 出力変数と評価項目 Output Variables and Validation Items
今回のシミュレーションでは, 空間中の電子に対して 次の値の時間推移を Particle-PLUS から出力した.
- 磁気モーメント $\mu$
- 運動エネルギー $K$
- 電子が受ける磁場 $\vec{B}$
- 磁場に平行な方向の速度 $\vec{v}_{/\!/}$
- 磁場に垂直な方向の速度 $\vec{v}_{\perp}$
- ピッチ角 $\theta$
可視化を含めたポスト処理全般には gnuplot[参考8] を用いている. 主に次の事項に着目して可視化を行った.
- $\mu$ と $K$ が一定となるかどうか
- ミラー効果で電子が閉じ込められるかどうか(位置空間プロット)
- ミラー効果で電子が反射する場合, その位置で 式(6) を満たすかどうか
- ロスコーン領域の可視化(速度空間プロット)
. シミュレーション結果 - 電子1つの解析 Analysis of Single Electron
位置空間における電子1つの軌跡を下の動画に示す. また, そのときの速度成分 $(v_{/\!/}, v_{\perp})$ の時間推移と, ピッチ角 $\theta$ の時間推移を, その下の図に示す. 電子が $B$ の強い領域に近づくにつれて $\theta$ が大きくなり, $\theta = 90°$($v_{/\!/} = 0\,$)となる位置で旋回中心の進行方向が反転する様子が観察された. この電子はミラー効果により効率的に閉じ込められている, と言える.
▲ [動画] 位置空間での軌跡 - (X,Y)表示
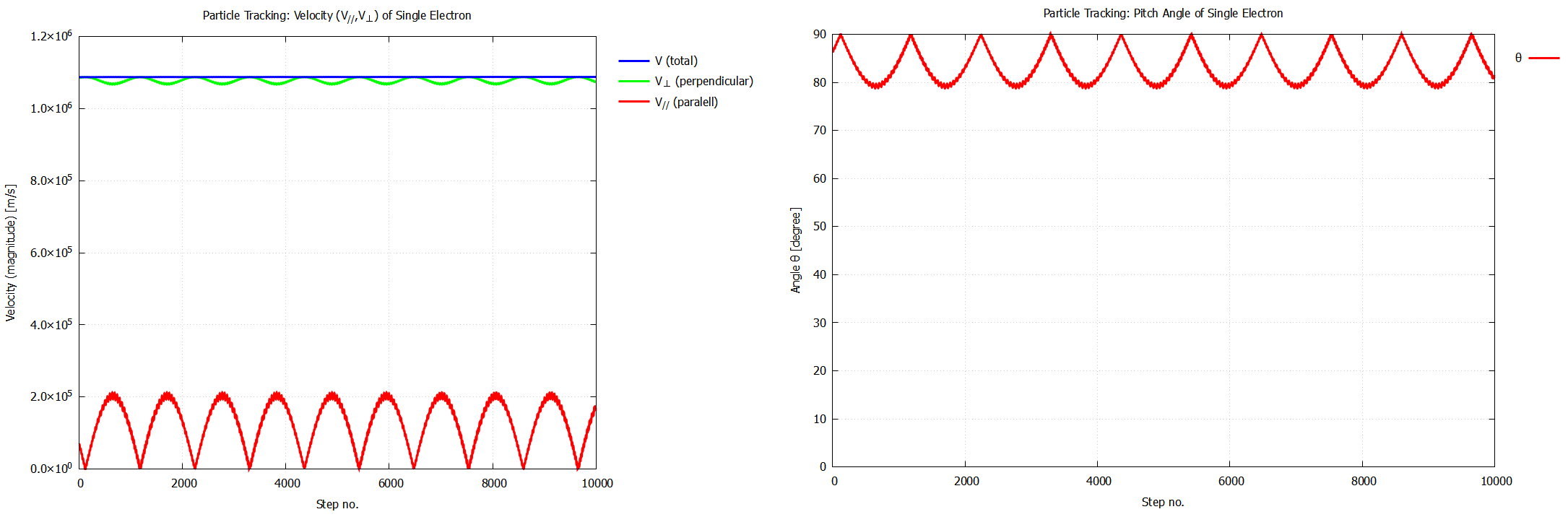
▲ (左図) 速度成分($v_{/\!/}$, $v_{\perp}$)の時間推移 ▲ (右図) ピッチ角 $\theta$ の時間推移
時間推移グラフの横軸に示されている時間ステップは, 1つ分の長さが 3×10-11 秒で一定である.
右図縦軸の θ=0° は磁場に平行, θ=90° は垂直である事を示す.
次に運動エネルギー $K$ と磁気モーメント $\mu$ の時間推移を下図に示す. どちらも長時間平均で見ると一定となっており, 良い保存量である事が確認された.
なお $\mu$ に関しては, 短い周期 1.35×10-9 秒で振動する成分が観測された. この振動周期は, $B$ の値から計算される電子の旋回周期に一致する. この周期よりも短い時間スケールでは, 電子の受ける $B$ が(磁石からの距離に応じて)大きく変化するために, それに合わせて $\mu$ も変化するものと理解される. 不変となる条件に関しては 3.2節 で触れている. 同様の振動成分は約1060step(3.2×10-8 秒)の周期でも観測されており, これは旋回中心の磁場方向に沿ったバウンス振動に該当する[参考7]. 以降の結果に影響が無いため, $\mu$ に関するこれらの振動成分は無視する.
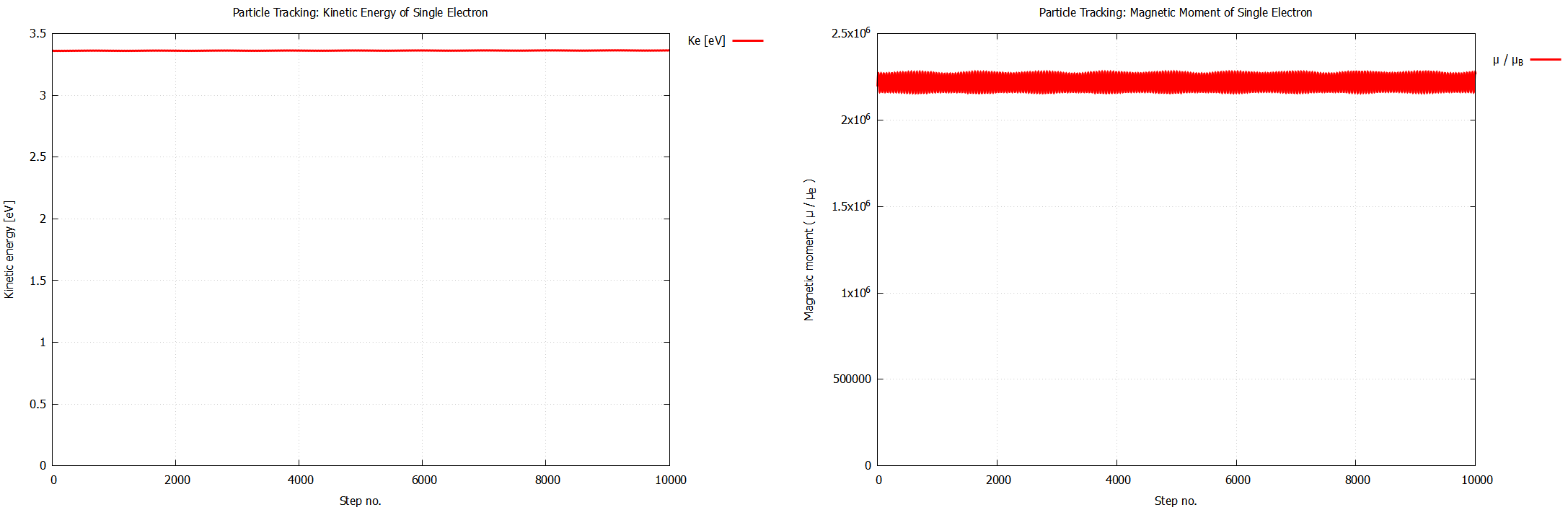
▲ (左図) 運動エネルギー $K$ の時間推移 ▲ (右図) 磁気モーメント $\mu$ の時間推移
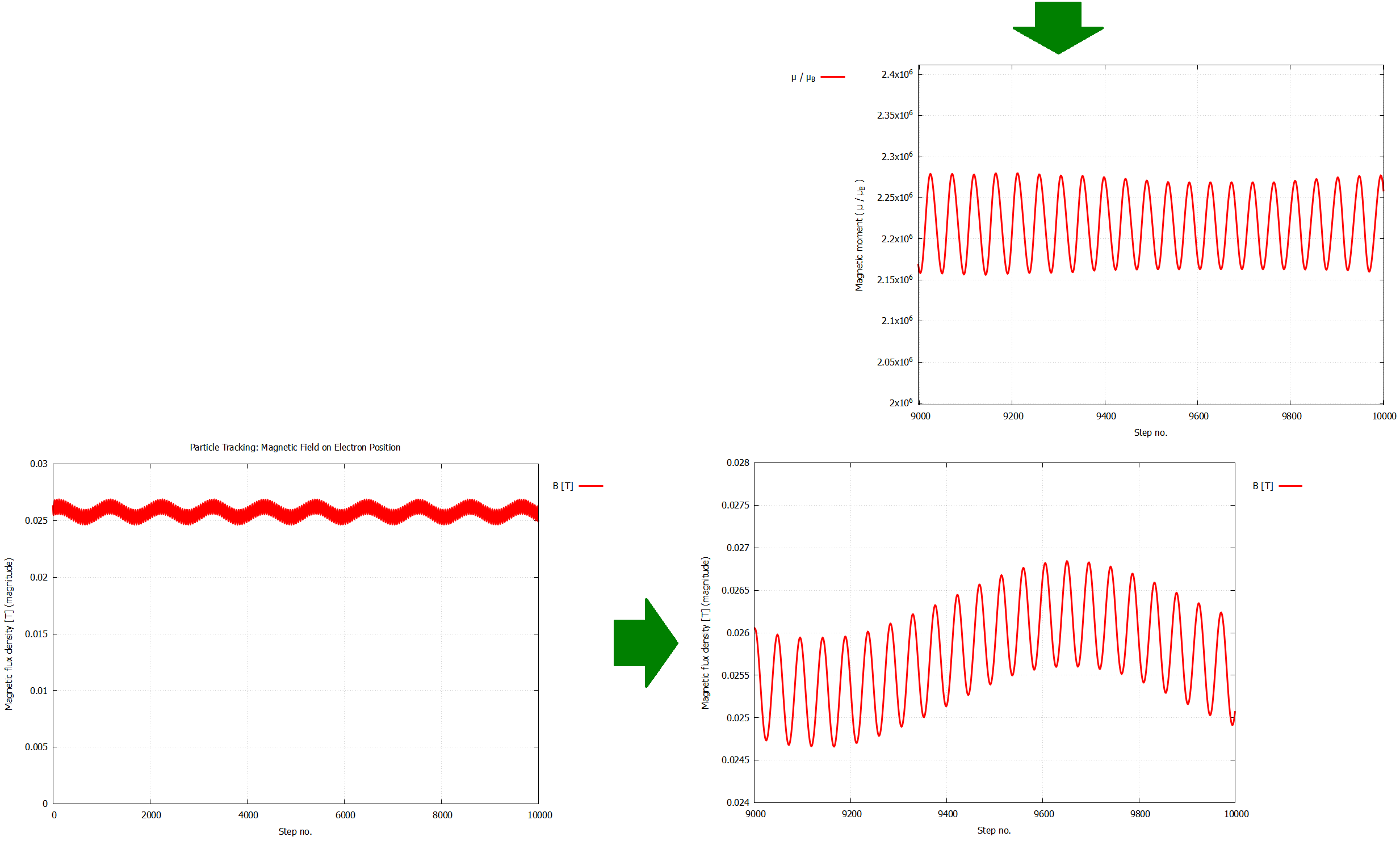
▲ (左図) 粒子が受ける磁場強度 $B$ の時間推移 ▲ (右図) $B$ と $\mu$ の拡大図
. シミュレーション結果 - 複数電子の解析 Results for Multiple Electrons
電子の初期位置が異なると, 受ける $\vec{B}$ も変わる. また, 異なる磁束線では $B_0$ と $B_1$ の値が変わるため, 必要となるミラー比, および確保可能なミラー比の値も変わる. これはロスコーンの分析を困難にする. そこで, 6.2節では初期位置が近い電子のみを取り出して分析している. 一方で, 6.1節では様々な位置での電子について, 粒子運動論から得られる 式(6) の再現性を検証している.
 6.1. 初期位置が異なる複数電子
6.1. 初期位置が異なる複数電子
ミラー効果で捕捉された電子10個について, 定義に従って求められる $R:=B_1/B_0$ の値と, 最小ピッチ角から求められる $R_0:=1/ \sin ^2 \theta _0$ との値を比較した. すると, 両者の値は誤差0.5%の範囲内で一致した. 下の図はその計算表の抜粋である. これらの結果より $R=R_0$ , すなわち 式(6) はシミュレーション上で高い精度で成り立つ事が分かった.
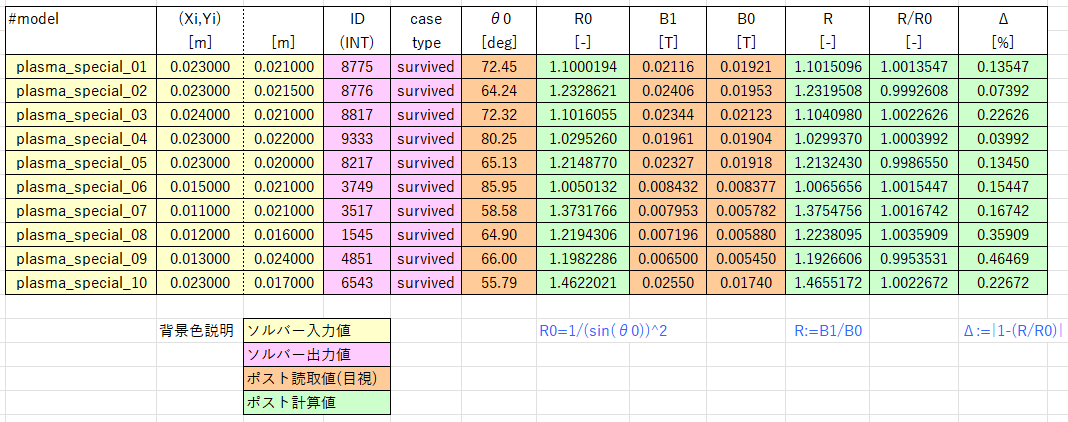
▲ 捕捉電子10個に対する $R/R_0$ の計算表
▲ [動画] 異なる位置・異なる速度で捕捉された電子の軌跡
見やすさを考慮して電子6個のみを表示している. 位置や速度が異なると旋回半径やピッチ角も様々な値を取るようになるが, 前述のように 式(6) は成立する.
 6.2. 初期位置が近い複数電子
6.2. 初期位置が近い複数電子
本節では新たな電子サンプル199個を用いた. そのうち無作為にピックされた20個について, 位置空間と速度空間での軌跡を下の動画に示す. 橙色の軌跡は磁場で捕捉された電子(8個)を表しており, 青色の軌跡は損失した電子(12個)を表している. Y = 1mm の位置に壁面が存在しており, そこへ到達した電子は空間から消滅する. ピッチ角の小さい粒子は空間中で $\theta = 90°$ ($v_{/\!/} = 0\,$) に到達する事ができず, 時間経過で消滅する様子が観察された.
▲ [動画] 位置空間での軌跡 - (X,Y)表示
▲ [動画] 速度空間での軌跡 - ($v_{/\!/}$, $v_{\perp}$)表示
見やすさ重視のために電子20個のみを表示している.
速度空間の図は縦軸を $v_{/\!/}$ にとっており, 天頂角が $\theta$ を表す.
次に, 各電子で $\theta$ が最小となる点を下図の速度空間上にプロットした. 薄い青色の点は左側のミラーで損失する電子(20個), 濃い青色の点は右側のミラーで損失する電子(43個), 橙色の点は捕捉電子(136個)を表す. 本シミュレーションでは, 左側と右側で空間磁場の強度が異なる(左側のほうが強い. 2章参照)ため, ロスコーン角は2つあると考えられる. 磁束線上の空間磁場強度の最小値, 最大値から見積もられるロスコーン角は, 左側で36.5°, 右側で47.5°であった. 図ではそのロスコーン領域の境界も点線で図示している. 損失する電子はロスコーン領域に含まれている事が確認された.
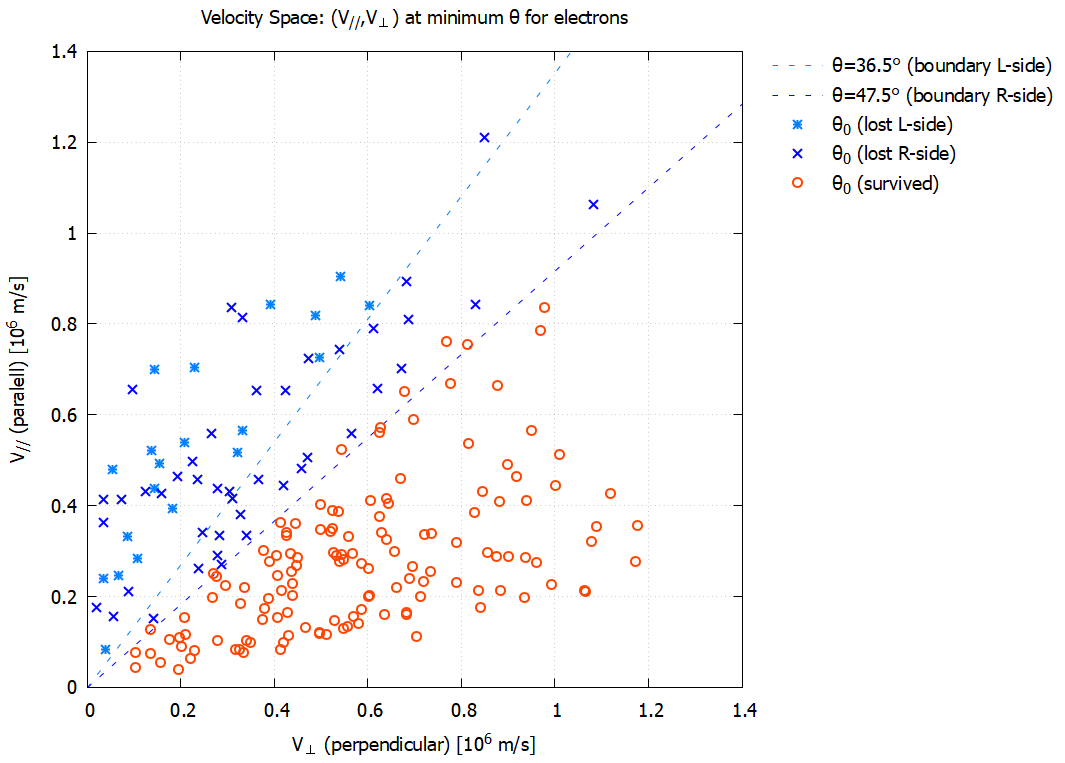
▲ ピッチ角が最小($\theta = \theta _0$)となる瞬間の速度とロスコーン境界
なおロスコーン角 47.5°付近では, 判定結果に 2°~3°程度の誤差が生じている. これは, らせん運動の旋回半径が有限の大きさを持つ事に起因しているとみられ, 考えられる理由として, (1) たとえ同じ位置から運動を開始したとしても, 旋回中心の沿う磁束線は電子ごとに異なる, (2) らせん運動の軌道と旋回中心の軌道では, 表面への到達時刻やその付近で受ける磁場強度が異なる, 等が挙げられる.
. まとめ Summary
付録. 理論式の導出 Appendix of Theoretical Formulas
本節での導出は簡易的な証明に留めている. より厳密な証明に関しては教科書等の他の文献を参照されたい[参考1,9].
添字 ${\rm c}$ , $0$ , $1$ については 3.1節 で説明されているが, 今回のシミュレーション結果を用いて改めて図に示すと次のようになる.
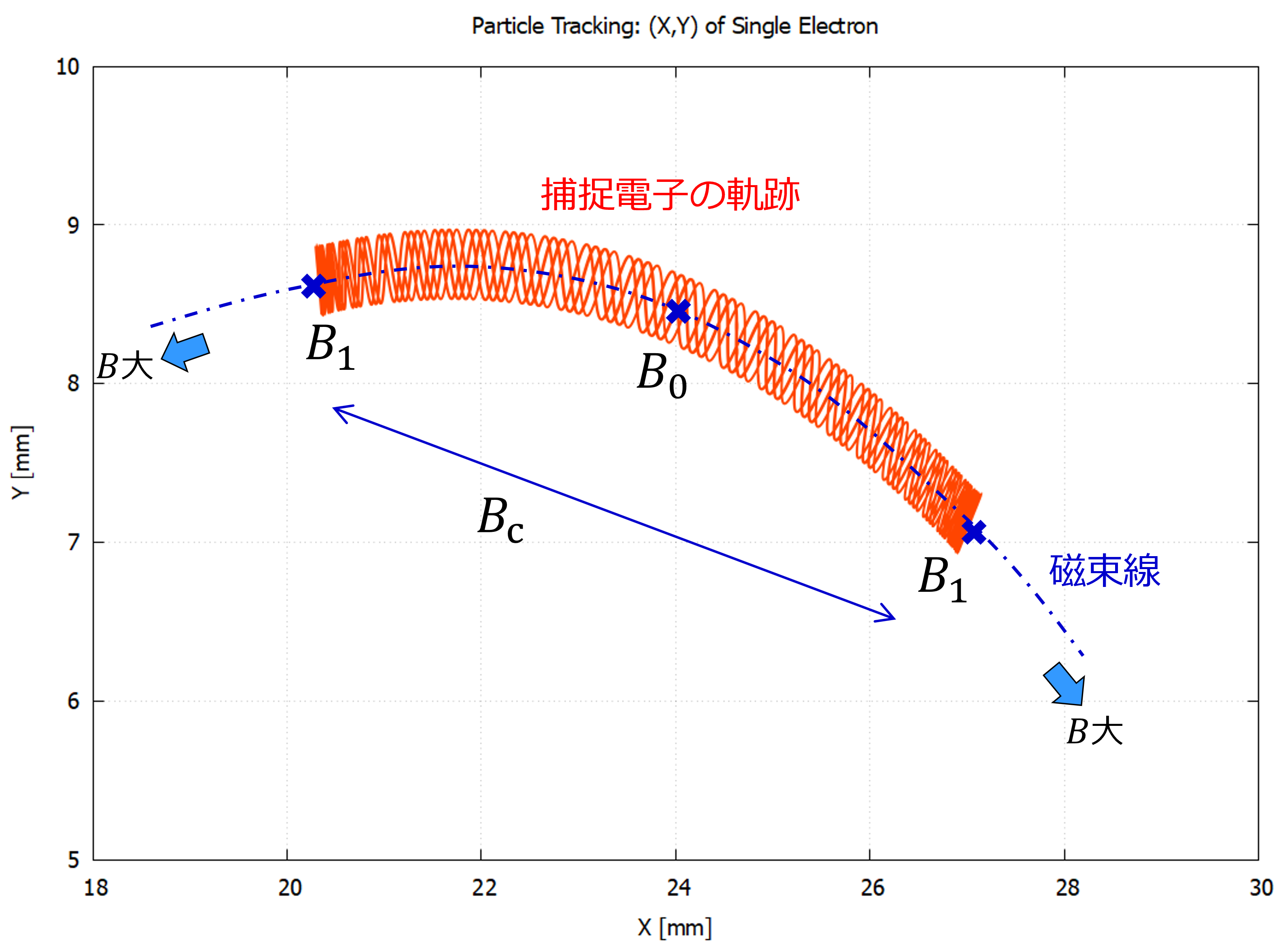
▲ 添字が示す位置
 付録1. ミラー比と最小ピッチ角との関係式(6)の導出
付録1. ミラー比と最小ピッチ角との関係式(6)の導出
ある磁束線に沿ってミラー効果で反射を繰り返す荷電粒子を考える. 粒子の受ける磁場が最小・最大となる位置(添字 $0$ と $1$ )について, $\mu$ と $K$ の不変性を立式する. \begin{align*} \frac{{v_0}^2_\perp}{B_0} &= \frac{{v_1}^2_\perp}{B_1} \\ \\ v_0^2 &= v_1^2 \\ &= {v_1}^2_{\perp} + {v_1}^2_{/\!/} \\ &= {v_1}^2_{\perp} \quad (\because \; v_{1/\!/} = 0) \end{align*} これら2つの式から $v_{1\perp}$ を変数消去すると次式が得られる. $$\frac{B_1}{B_0} = \frac{v_0^2}{{v_0}^2_\perp}$$ 左辺は $R$ の 定義式(4) に等しい. 右辺は $\sin \theta = v_\perp/v$ である事を用いて $\theta _0$ で書き換えられる. すると, $$R = \frac{1}{\sin ^2 \theta _0}$$ が得られる.
 付録2. ミラー磁場による閉じ込め条件(3.3節)の導出
付録2. ミラー磁場による閉じ込め条件(3.3節)の導出
ある磁束線上の荷電粒子の位置(添字 ${\rm c}$ )と, 磁場が最小となる位置(添字 $0$ )について, $\mu$ と $K$ の不変性を立式する. \begin{align*} \frac{{v_0}^2_\perp}{B_0} &= \frac{{v_{\rm c}}^2_\perp}{B_{\rm c}} \\ \\ v_0^2 &= v_{\rm c}^2 \\ &= {v_{\rm c}}^2_{\perp} + {v_{\rm c}}^2_{/\!/} \end{align*} これら2つの式から $v_{{\rm c}\perp}$ を変数消去すると次式が得られる. $${v_{\rm c}}^2_{/\!/} = v_0^2 - \frac{B_{\rm c}}{B_0} {v_0}^2_\perp$$ ここで, ${v_{\rm c}}^2_{/\!/} \ge 0$ が実数解を持つためには, \begin{align*} v_0^2 - \frac{B_{\rm c}}{B_0} {v_0}^2_\perp & \ge 0 \\ ⇔ \quad \frac{B_{\rm c}}{B_0} & \le \frac{v_0^2}{{v_0}^2_\perp} \\ ⇔ \quad \frac{B_{\rm c}}{B_0} & \le R \end{align*} が満たされなければいけない. これはすなわち, 荷電粒子が $\mu$ を一定に保ちながら運動するためには, 受けることのできる $B_{\rm c}$ には上限が存在し, $B/B_0 > R$ の強磁場領域へは侵入できない事を意味する.
 付録3. ロスコーン範囲(3.4節)の導出
付録3. ロスコーン範囲(3.4節)の導出
ある磁束線上の荷電粒子の位置(添字 ${\rm c}$ )と, 磁場が最大となる位置(添字 $1$ )について, $\mu$ と $K$ の不変性を立式する. \begin{align*} \frac{{v_{\rm c}}^2_\perp}{B_{\rm c}} &= \frac{{v_1}^2_\perp}{B_1} \\ \\ v_{\rm c}^2 &= {v_1}^2_\perp \end{align*} 2つの式から $v_{1\perp}$ を変数消去すると次式が得られる. \begin{align*} \frac{v_{\rm c}^2}{{v_{\rm c}}^2_\perp} &= \frac{B_1}{B_{\rm c}} \\ &= R \frac{B_0}{B_{\rm c}} \end{align*} ここで, 添字の定義(上図参照)より $B_0 \le B_{\rm c}$ なので, $$\frac{v_{\rm c}^2}{{v_{\rm c}}^2_\perp} \le R$$ が満たされなければいけない. 両辺をピッチ角でそれぞれ表し, 角度範囲が $0 \le \theta \le 90°$ である事も考慮すると, \begin{align*} \frac{1}{\sin ^2 \theta _{\rm c}} & \le \frac{1}{\sin ^2 \theta _0} \\ ⇔ \quad \frac{\sin ^2 \theta _{\rm c}}{\sin ^2 \theta _0} & \ge 1 \\ ⇔ \quad \frac{\sin \theta _{\rm c}}{\sin \theta _0} & \ge 1 \\ ⇔ \quad \frac{\theta _{\rm c}}{\theta _0} & \ge 1 \end{align*} が得られる. これが閉じ込められる条件であるため, 逆に損失する $\theta$ の範囲は, $$ \frac{\theta}{\theta _0} \lt 1 $$ である.
補注 Notes
- 3次元速度ベクトルが等方性のマクスウェル-ボルツマン分布[参考10] (Maxwell-Boltzmann Distribution[wikipedia↗])に従うとしている. これらの電子群はモンテカルロ法(Monte Carlo Method[wikipedia↗])で生成されている.
- マクスウェル電磁気学における $\vec{B}$ は, 正確には磁束密度(Magnetic Flux Density[wikipedia↗])と呼ばれる量である. 本記事では磁場強度(Magnetic Field Strength)$\vec{H}$ が登場しないため, ここでは $\vec{B}$ を単に「磁場」と呼んでいる.
- この回転運動は, サイクロトロン運動(Cyclotron motion), ジャイロ運動(Gyromotion), ラーモア運動(Larmor motion)等と呼ばれる. いずれの用語も「磁場で誘起される荷電粒子の回転運動」を意味する上では, 本質的に大きな違いは無い. サイクロトロンは粒子加速器に由来する用語であり, 重心の軌跡に着目する場合が多い. ジャイロは角運動量保存則のために回転軸が歳差運動する現象, いわゆるジャイロ効果全般を指す. ラーモアは磁気モーメントに関する歳差運動の発見者である. 混乱を避けるために, 本記事ではなるべく「旋回」という用語に統一させている.
- 外部パラメータに依存するハミルトン系であっても, ハミルトニアン(Hamiltonian[wikipedia↗])の変化が小さければ断熱的であるとみなして良い. ここで, 歴史的な経緯で「断熱(Adiabatic)」という語が使用されているが, ハミルトニアンの変化が無いわけではないため, 誤解を生みやすい表現ではある. 現代の物理学で言うところの準静的過程(Quasistatic Process)の状況に近いと思われる[参考11].
- ここでの「Bが緩やかに」とは, 旋回周期に対して時間的および空間的にBの変化が小さい事を意味する[参考9].
- ここではピッチ角の定義域を 0≤θ≤ 90° としているが, 文献によっては 0≤θ≤180° で定義されているものもある. もし運動方程式ベースで議論する際は, 後者が扱いやすいであろう. 本記事の内容は保存則ベースでの議論が可能であり, またミラー効果における粒子捕捉/損失の結果は θ=90° を境にして対称である(3.4節 で示したロスコーンは鏡面対称である)ため, ここでは 3.3節 で示した定義で十分である.
参考資料 References
- F. F. Chen 「プラズマ物理入門」, 内田岱二郎 訳, 丸善 (1977)
- T. Motomura and T. Tabaru, Vacuum and Surface Science, Vol.63, No.6 (2020) 283-288
- H. Akimune, T. Yamagishi, I. Ikeda and F. Okamoto, Kakuyugo Kenkyu, Vol.42, No.4 (1979) 472-531
- Y. Miyoshi et al., J. Plasma Fusion Res. Vol.97, No.5 (2021) 269-275
- 株式会社ウェーブフロント 「Particle-PLUS」, https://www.wavefront.co.jp/CAE/particle-plus/[リンク↗]
- 長倉三郎, 井口洋夫, 江沢洋, 岩村秀, 佐藤文隆, 久保亮五 「岩波 理化学辞典」, 岩波書店 (1998)
- S. Shinji, NICT Reports, Vol.67, No.1 (2021) 105-113
- T. Williams and C. Kelley 「gnuplot」, http://www.gnuplot.info/[リンク↗]
- 電気学会, 電気学会大学講座シリーズ 「プラズマ工学」, オーム社 (1997)
- 株式会社ウェーブフロント, コラム 「プラズマ・流体シミュレーションの基礎」, https://www.wavefront.co.jp/CAE/particle-plus/column/plasma_simulation_basic.html[リンク↗]
- 予備校のノリで学ぶ大学の数学・物理 「断熱不変量(古典力学系)」, YouTube (2019), https://www.youtube.com/watch?v=3QBghN-QwQ8[リンク↗]
 |
佐橋 一裕(株式会社ウェーブフロント 連成問題研究部)
愛知県生まれ. 私立東海中学校・高等学校を卒業.
名古屋大学大学院にて修士号(理学)を取得後, ウェーブフロントへ入社.
大学院時代に極低温実験による量子物性研究, 入社後に青色/白色LEDの解析業務を経て,
現在はプラズマ解析に関するソフトウェア開発・コンサルティング・技術サポート等の業務に従事している.
|