概要
 ベイズ最適化とは
ベイズ最適化とは
工学設計においては、目的関数(達成したい性能)と設計変数(設計時に変更可能な値)の関係が自明である場合は殆ど無く、
実験やシミュレーションを通して目的関数と設計変数の関係を求めることとなります。
しかしながら、このような実験やシミュレーションには、多大なコストと計算時間が必要とされます。
実験やシミュレーションの回数をできる限り少なくするためには、目的関数を近似しながら最適化を行うモデル予測最適化(モデルベース最適化とも称す)が、大きな威力を発揮します。
ベイズ最適化は、この逐次近似モデルを使用する最適化の1つであり、少ないデータで精度の高い最適値を高速に予測することが可能です。
 適用事例
適用事例
弊社では以下のような適用事例がございます。
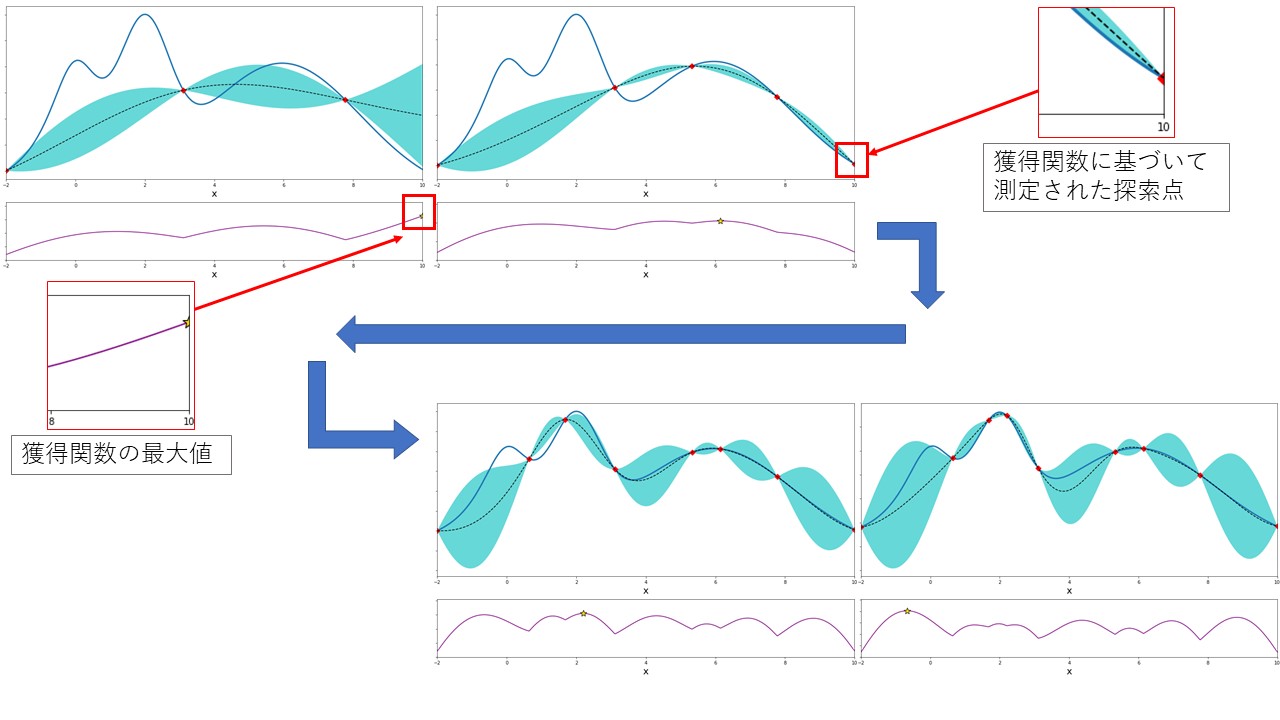
図1 ガウス過程回帰による事後確率分布の推定結果 (青の実線:真値、青の点線:期待値、青の塗り潰し:分散、紫の実線:獲得関数)
獲得関数の最大となる点を次ステップにおける探索点としてシミュレーションまたは実験を実施します。その結果をこれまでのデータに追加し、新たに事後確率分布を推定します。この手順を繰り返すことにより、最適解を与える設計変数を推定します。 上図より、事後確率分布がステップ毎に真値に近づいて行く様子が良くわかります。 また、ガウス過程回帰は多峰性の分布も精度良く近似できることがわかります。
説明
 逐次近似モデル
逐次近似モデル
ベイズ最適化では、N点の入出力データ(x1, f(x1))・・・・(xN, f(xN))が得られた時、ガウス過程回帰に基づき、出力データ:f(x)を近似する関数を、事後確率分布の形で推定します。(すなわち、期待値と標準偏差の分布を推定します。)
実験やシミュレーションによるN+1回目のデータ取得に際しては、最適値を与えると予測される探索点:xN+1 をどこに定めれば良いかを、逐次近似モデルを使用して決定します。
 最適値の探索
最適値の探索
ガウス過程回帰では、入出力を近似する関数の推定結果は、事後確率の期待値と標準偏差の分布として得られます。
次ステップの真の最適解の探索は、期待値と標準偏差を組み合わされて定義された獲得関数(Acquisition Function)が最大となる点:xN+1として定義されます。
- 単一目的関数の探索では、信頼性上限関数(Upper Confidence Bound)や期待改善度(Expected Improvement:EI)が獲得関数として使用されます。
- 多目的関数の探索では、ハイパーボリューム期待改善度(Expected Hyper Volume Improvement:EHVI) や最大期待改善度(Expected Maximum Improvement: EMI)が獲得関数として使用されます。EHVIでは、目的関数空間におけるハイパーボリュームを最大化するように探索点を決定します。
 ベイズ最適化の特徴
ベイズ最適化の特徴
ベイズ最適化では、目的関数の最適解を与える設計変数の探索に、ガウス過程回帰に基 づく逐次近似モデルを使用するため、探索が高速です。また、進化型最適化アルゴリズ に比べて探索点の数も少なく、効率的に最適解を求めることが可能です。 逐次近似モデルを使用しないNSGA-Ⅱ等の進化型最適化アルゴリズムに比べると、 実験やシミュレーションによるコストおよび計算時間の大幅な短縮が可能となります。