予測する変数が二値(正常/異常)であることから、分類モデルを選択します。

ここでの目的は、流量計測過程における種々の特性値を入力として、超音波流量計が故障する確率をモデル化することです。

最初のステップは、近似モデルの情報源であるデータセットの準備です。 データセットは以下で構成されています。

• データソース
• 変数
• インスタンス

8つの経路を有する液体超音波流量計に対する、37個の診断パラメータを持つ87個のインスタンスが含まれています。 これらの36個の変数は、ターゲットである"稼働状態"を除いてすべて連続です。 変数は以下の通りです。

入力

• フラットネス比
• 対称性
• クロスフロー
• 8つの経路それぞれの流速
• 8つの経路のそれぞれの音速
• 8つの経路の平均音速
• 8つの経路の両端のゲイン

ターゲット

• 稼働状態(正常/異常)

ニューラルネットワークが扱うのは数値なので"稼働状態"は、流量計が故障している場合は0、正常に動作している場合は1という2つの数値に変換されています。

データを準備したら、学習で考慮すべき要素を抽出し可視化します。 まずは、データセットに含まれる陰性(異常)の事例と陽性(陽性)の事例の比率を知ることが重要です。 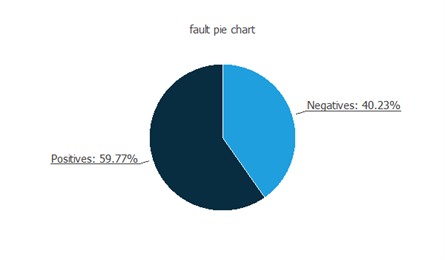上のグラフは、陰性(異常)なインスタンスの数(40.23%)と陽性(正常)なインスタンスの数(59.77%)が同程度であることを示しています。 この情報は、後に予測モデルを適切に設計するために使用されます。

次の図は、各入力とターゲットの間の相関関係を分析したものです。 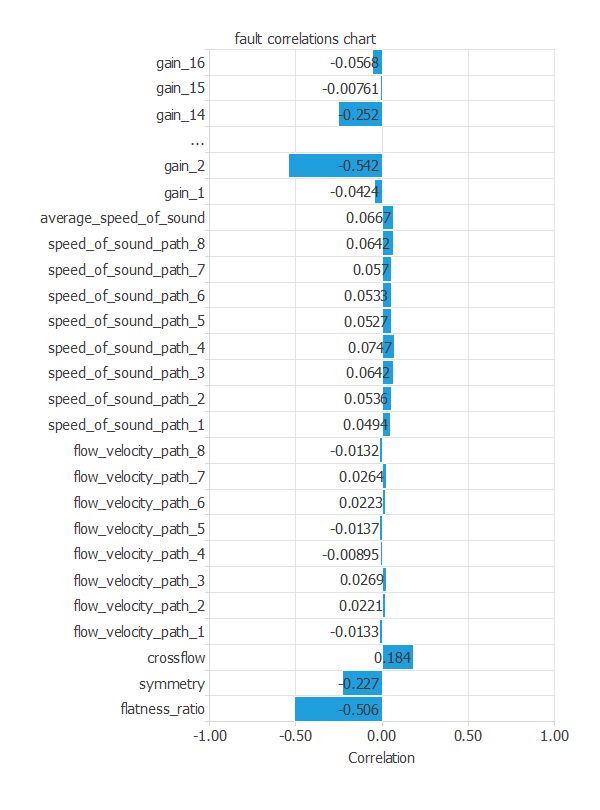"flatness_ratio: フラットネス比"("-0.506)といくつかの"gain_i: ゲイン"が、最もターゲットとの相関の強い入力だと分かります。 一方で、経路内の流速の相関は非常に弱いため、流量計の稼働状態を予測する上で決定的要素とはなりません。

このデータセットをランダムに分割し、87個のインスタンスの内、53個(60％)を訓練用、17個(20％)のを検証用、17個(20％)をテスト用とします。

次のステップはニューラルネットワークの構造の設定です。 分類モデルでは通常、ニューラルネットワークは次のように構成されます。

• スケーリング層
• パーセプトロン層
• 確率層

スケーリング層

スケーリング層は、入力の統計情報とスケーリング手法を含みます。

パーセプトロン層

この例では、入力が36個、ニューロン数が3個の層を1つ用います。

確率層

確率層では、確率として解釈できるよう、各出力が0から1の間の値をとり、それらの和が1になるように変換します。

次の図は、この例のニューラルネットワークの構造を示しています。 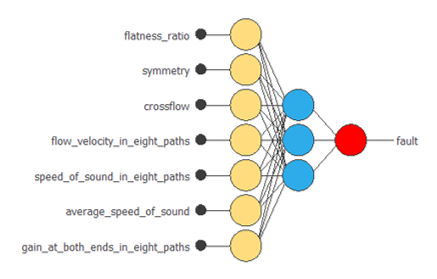ただし、8本の経路それぞれに対する入力はまとめて1つのノードで表しています。

次のステップは、ニューラルネットワークが何を学習するかを規定する、学習手法の選択です。 一般的な学習手法は、2つのコンセプトで構成されています。

• 損失関数
• 最適化アルゴリズム

損失関数

この例のデータセットの異常/正常のバランスは少し悪いですが、損失関数として正規化二乗誤差とL2正則化を選択しました。

最適化アルゴリズム

最適化アルゴリズムには、今回のような例でのデフォルト設定である、準ニュートン法を採用しました。

次のグラフは、学習過程において、訓練誤差(青)と検証誤差(オレンジ)がエポック数(学習の繰り返し回数)に応じて減少する様子を示しています。 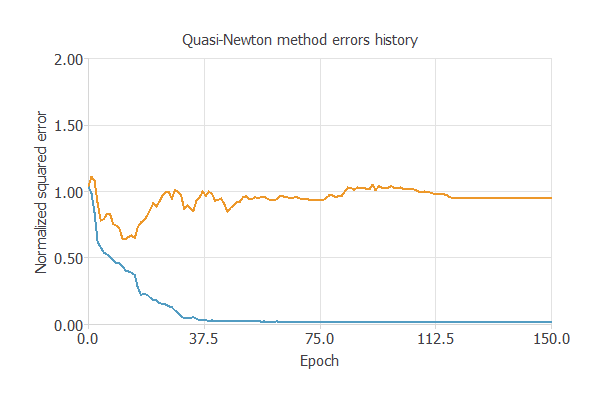最終的な値は、訓練誤差＝0.0161NSE、検証誤差＝0.954NSEです。 この検証誤差は信頼できる値ではありません。したがって、これを改善するためにモデル選択プロセスを行う必要があります。

モデル選択の目的は、最良の汎化性能を持つネットワーク構造を見つけること、すなわち、検証誤差を最小化することです。 具体的には、検証誤差が上で達成した値(0.954NSE)を下回るネットワーク構造/パラメータを探索ことです。

入力の数が多すぎるので、入力数選択アルゴリズムを使って、いくつかの変数を"未使用"にします。 入力数選択アルゴリズムの1つであるグローイングインプットでは、少ない入力数から始めて、学習を繰り返すごとに入力数を増やしていきます。 次の図は、訓練誤差(青)と検証誤差(赤)を、エポック数(学習の繰り返し回数)ごとの入力数の関数として示しています。

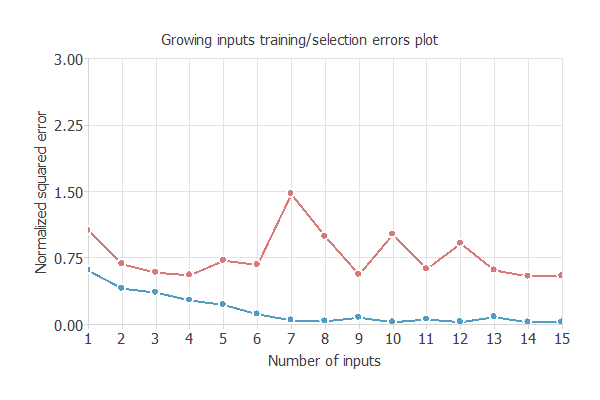
また、ニューロン数選択アルゴリズムでは、ニューロン数を変えながら学習を反復し、検証誤差が最も小さいものを選択します。 その一種のグローイングニューロンでは、少ないニューロン数から始めて、反復するごとにニューロン数を増やしモデルの複雑性を増していきます。 次の図は、訓練誤差(青)と検証誤差(黄)を、エポック数(学習の繰り返し回数)ごとのニューロン数の関数として示しています。

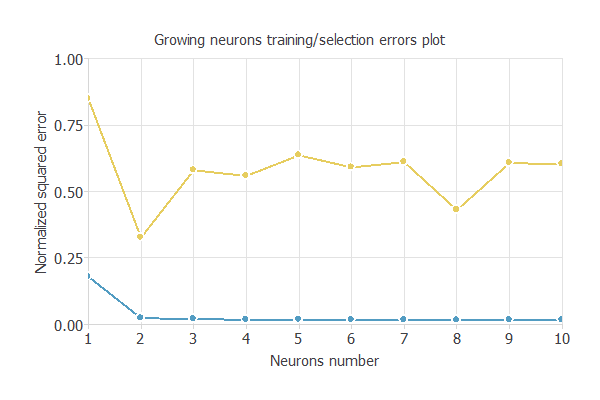
結果として得られる新しいネットワークアーキテクチャは次の図のようになります。 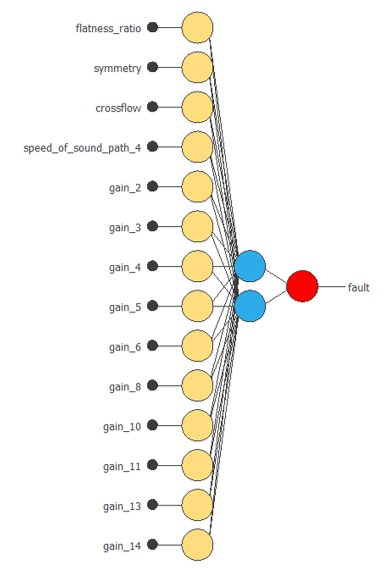モデル選択を経て最適化されたモデルでは、入力が14個、パーセプトロン層のニューロン数が2個になりました。 この構成での検証誤差は0.326NSEにまで減少しました。

二値分類モデルの精度を測るのに良い指標の1つが、下の図のようなROC(Receiver Operating Characteristic: 受信者操作特性)曲線です。 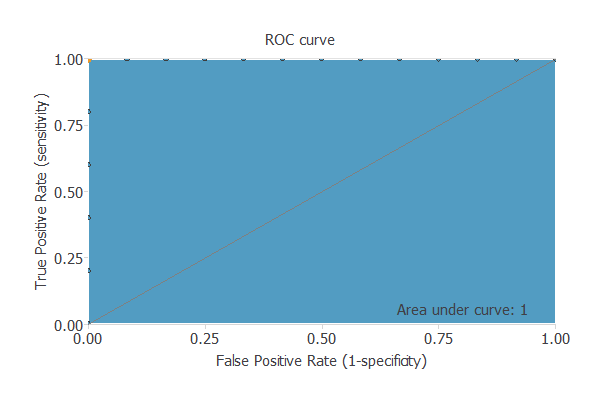ここでの重要な値は、AUC(Area Under the Curve: 曲線下面積)です。 この例では、最大の値であるAUC=1をとっており、全て正しく判断していることを示しています。

もう一つの指標として、混同行列があります。 この行列は、出力値/実際の値が陽性/陰性に値をとるインスタンスの個数を表しています。 対角成分の値が、出力値と実際の値が等しい、つまり、正しく予測できているインスタンスの個数となります。 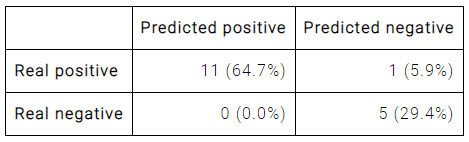上の混同行列から、

• 分類精度(正しく分類されたインスタンスの割合): 94.12%
• エラー率(誤って分類されたインスタンスの割合): 5.88%
• 感度(実際に陽性のうち陽性と予測されたインスタンスの割合): 91.67%
• 特異性(実際に陰性のうち陰性と予測されたインスタンスの割合): 100%

という結果が見てとれます。 この結果から、正常品(陽性)よりも異常品(陰性)を見逃すことなく判別できる事が分かります。 目的は流量計の異常を検知することなので、これは良い結果だと言えます。

作成したモデルの信頼性/精度が確認できたら、このモデルを使って流量計の稼働状態をチェックすることができます。

また予測モデルは、機器の稼働状態を判断する際に最も重要な要素が何であるかを示すことができます。 これにより迅速な対応が可能となり、長期にわたってシステムの機能不全を回避できます。 一方で、正常に動作すると予測する場合には不要なメンテナンスを削減することで、経済的資源も大幅に節約できます。