DSMC-Neutrals 解析事例 - 真空ポンプの排気シミュレーション
DSMC-Neutralsはモンテカルロ直接法(Direct Simulation Monte Carlo Method;DSMC法)を用いた3次元希薄気体解析ソフトウェアです. 非構造メッシュを用いることにより,複雑な形状のシミュレーションが可能です. また,化学反応の計算も可能であり,真空チャンバー内の希薄なガス流れはもちろんのこと, 化学蒸着(Chemical Vapor Deposition;CVD)などの半導体製造における薄膜生成のシミュレーションにも適しています. 本記事を読んで希薄気体解析・ガス流れシミュレーションに少しでも興味をお持ちになりましたら 資料請求や 無料セミナーなど承りますので, いつでもお気軽にお問い合わせください.
はじめにIntroduction
DSMC-Neutralsは非構造メッシュを採用しているため複雑な形状の装置に対するシミュレーションが可能です.
そのため,例えばターボ分子ポンプとつながっている配管のコンダクタンスを評価することができます.
今回は単純化したモデルを用いて配管やオリフィスのコンダクタンスや真空槽内部の排気曲線(排気時間)の評価を行ってみます.
また,理論的に求めたコンダクタンス値や排気曲線との比較を行うことで,実際にシミュレーションを行うことの有用性を感じてもらえたらと思います.
短円筒配管のコンダクタンスと排気曲線Conductance and Pumping Time of Short Pipe
まず,本事例における基準モデルとして下図のような計算モデルを考えます. (便宜上このモデルを「standard」または「A」と呼ぶことにします.)
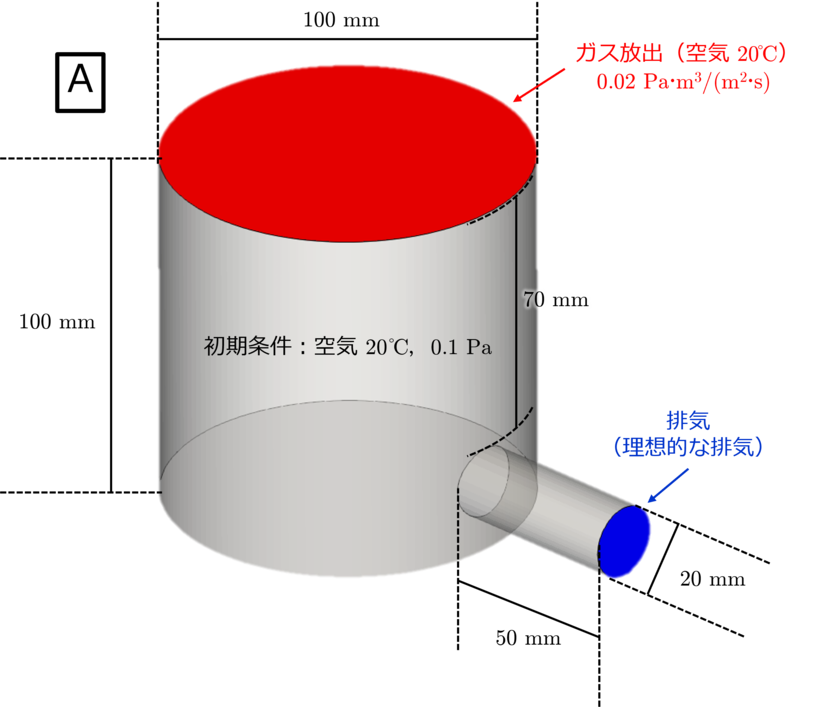
▲ 基準モデル(standard/A).
直径 $100\ \mathrm{mm}$ で高さ $100\ \mathrm{mm}$ の円筒型真空槽の側面に直径 $20\ \mathrm{mm}$ で長さ $50\ \mathrm{mm}$の短円筒配管がつながっていて,
配管の終端部(図中の青面)は真空ポンプにより理想的に排気(到達した気体分子がすべて排気)される状況を考えます*1.
また,真空槽への定常的な気体放出がある場合を考え,
$20^{\circ}\!\mathrm{C}$ の空気が $0.02\ \mathrm{Pa\cdot m^{3}/(m^{2}\cdot s)}$ で真空槽上部(図中の赤面)において支配的に容器内に加わるとします.
その他の条件として,真空槽および配管の壁温は $20^{\circ}\!\mathrm{C}$,
計算の初期条件(排気の初期圧力)は $20^{\circ}\!\mathrm{C}$ の空気 $0.1\ \mathrm{Pa}$ とします*2.
上記の条件で行った排気シミュレーションにより下図のような結果が得られました.
 |
 |
 |
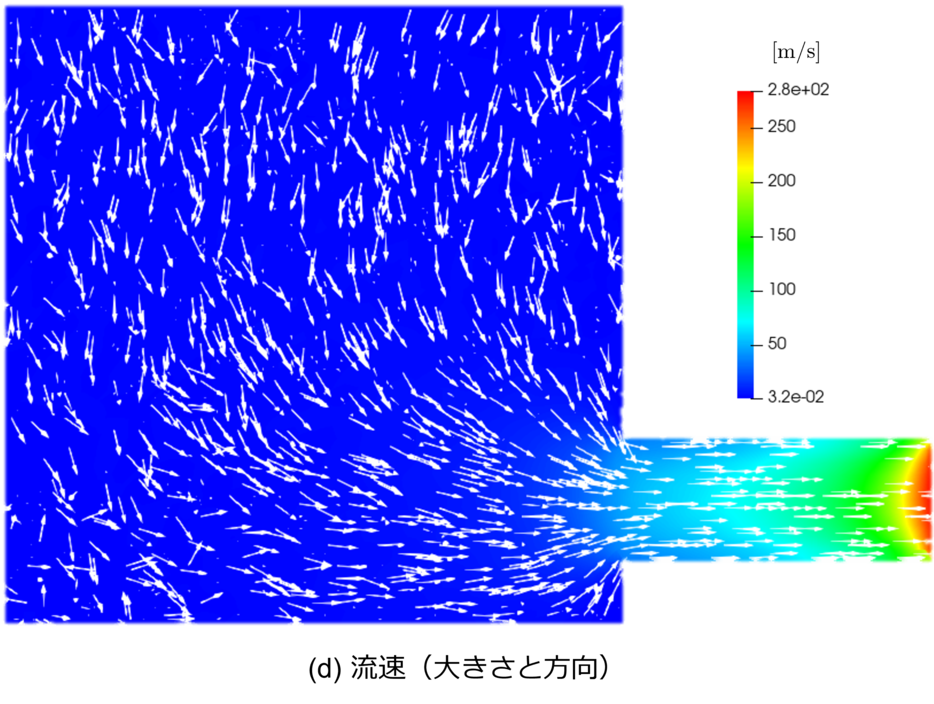 |
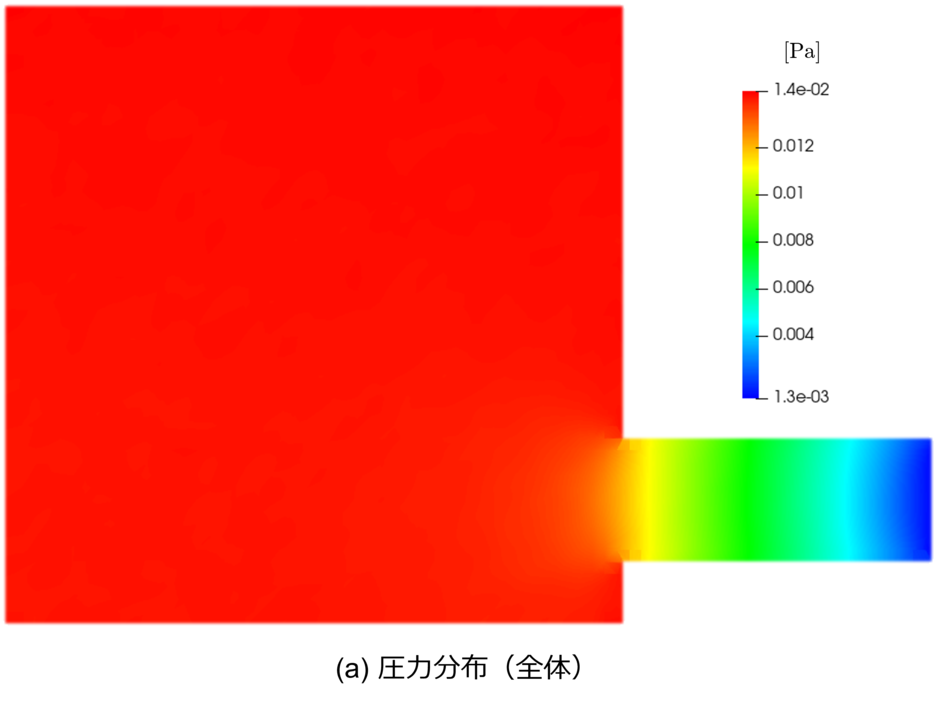
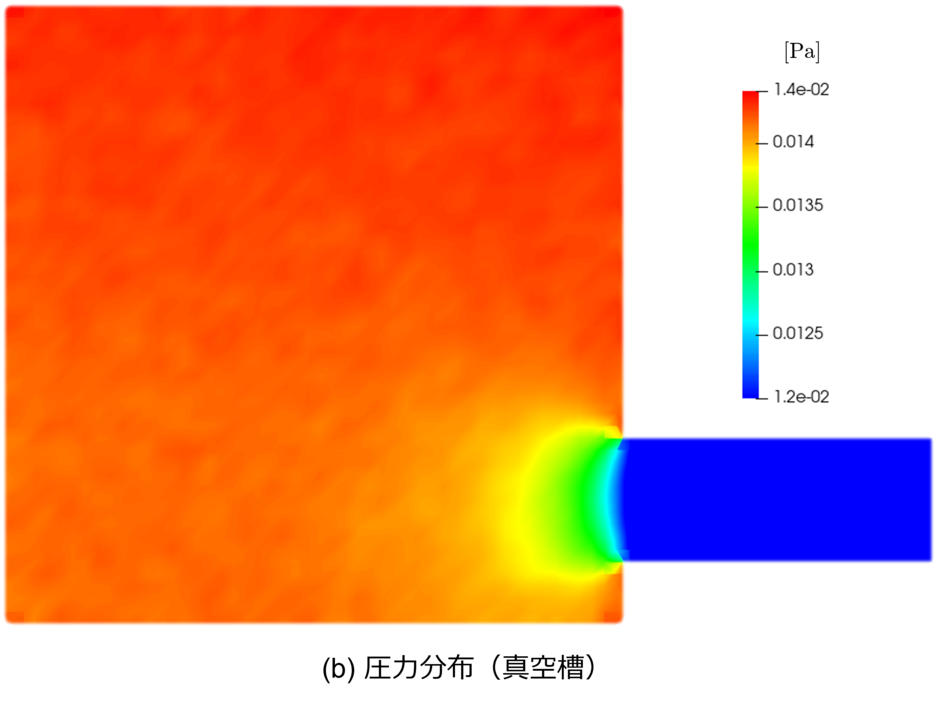
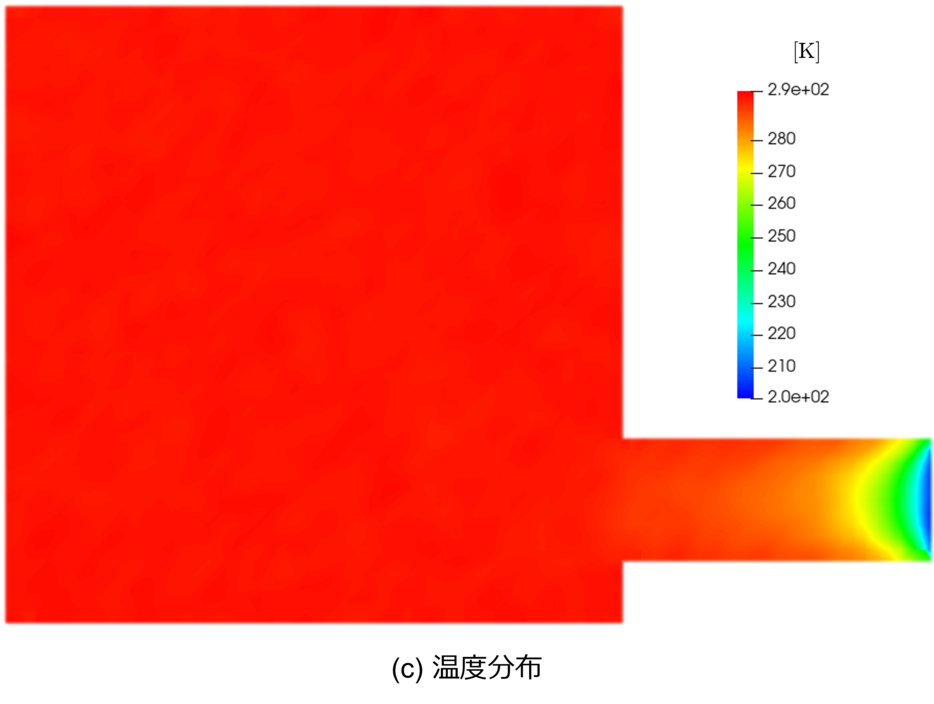
▲ 基準モデル(standard/A)における排気シミュレーション結果(断面図). (a) 圧力分布,(b) 真空槽内に着目した圧力分布,(c) 温度分布,(d) 流速(コンターは大きさ,白矢印は向きを表す).
配管内部は配管入り口から排気口に向かって線形に減圧している様子が分かります.
真空槽内部の圧力はほとんど一定ですが,厳密には槽内平均圧力比で ${+1.5\%}/{-15\%}$ の濃淡があることが分かります.
温度については排気口を除いてほとんど $20^{\circ}\!\mathrm{C}$ で一定です.
今回は理想的な排気を考えており,排気口付近では分子の速度が揃い(分散が小さくなり)ますので温度が小さくなります.
流速分布からも排気口付近では速度が揃っていることが推測できます.
さて,ここからはシミュレーション結果から短円筒配管のコンダクタンス $C$ を評価してみます.
配管入り口の圧力を $p_{\mathrm{in}}$,排気口の圧力を $p_{\mathrm{out}}$,排気速度を $S$ とすると,
\begin{align*}
C = \frac{Sp_{\mathrm{out}}}{p_{\mathrm{in}}-p_{\mathrm{out}}}
\end{align*}
により配管のコンダクタンスを求めることができますので,シミュレーション結果からモデルAの短円筒配管のコンダクタンスが
\begin{align*}
C \sim 0.0120\ \mathrm{m^{3}/s}
\end{align*}
であると評価できます.
一方で,分子流の場合のコンダクタンス $C_{\mathrm{f}}$ (下付きの $\mathrm{f}$ は formulated の意味)の表式はいくつかの場合で知られており,
例えば $20^{\circ}\!\mathrm{C}$ の空気に対する短円筒配管のコンダクタンスは
\begin{align*}
C_{\mathrm{f}} = K_{\mathrm{c}} \times 116A
\end{align*}
で求められます*3[1].
ここで,$K_{\mathrm{c}}$ はClausing係数と呼ばれ,配管の直径 $d$ と長さ $l$ の比 $l/d$ に対して決められる量です.
また,$A$ は配管の断面積 $\mathrm{(m^{3})}$ です.
今,$l/d=2.5$ に対して $K_{\mathrm{c}}=0.318$ とすると,
\begin{align*}
C_{\mathrm{f}} \sim 0.0116\ \mathrm{m^{3}/s}
\end{align*}
と求められます.
シミュレーションにより求めたコンダクタンス $C$ と理論式から求めたコンダクタンス $C_{\mathrm{f}}$ との間には相対的に $3.6\%$ の,
絶対的に $0.00041\ \mathrm{m^{3}/s}$ の差異があります.
これは,理論式においては配管内部で温度分布が生じることを想定していない点や,
真空槽内部が理想的に一様圧力ではない(真空槽自体のコンダクタンスを無視できない)ことなどから影響を受けた,
系統的な差異であると推測されます.
今度は排気速度について考えます.
真空槽に取り付けた配管及び真空ポンプの実行排気速度 $S_{\mathrm{e}}$ (下付きの $\mathrm{e}$ は effective の意味)は,
\begin{align*}
S_{\mathrm{e}} = \frac{SC}{S+C}
\end{align*}
と表せます.
したがって,シミュレーション(のみ)から求められる実行排気速度は
\begin{align*}
S_{\mathrm{e}} = 0.0105\ \mathrm{m^{3}/s}
\end{align*}
となります.
一方で,理論式により評価したコンダクタンスを用いると,
\begin{align*}
S_{\mathrm{e}}^{\prime} = \frac{SC_{\mathrm{f}}}{S+C_{\mathrm{f}}} \sim 0.0101\ \mathrm{m^{3}/s}
\end{align*}
となります.
実行排気速度の評価に用いたコンダクタンスの違いから,$S_{\mathrm{e}}$ と $S_{\mathrm{e}}^{\prime}$ の間には相対的に$3.1\%$の,
絶対的に $0.00032\ \mathrm{m^{3}/s}$ の差異があります.
実行排気速度を求めることができましたので,最後に排気曲線を描いてみましょう.
真空槽内部の圧力を $p$,容積を $V$,真空槽内へのガス放出量を $Q$ と書くと,排気方程式は
\begin{align*}
V\frac{\mathrm{d}p}{\mathrm{d}t} = -S_{\mathrm{e}}p + Q
\end{align*}
となります.
初期圧力が $p_{0}$ のとき,この微分方程式の解は
\begin{align*}
p(t) = \left( p_{0} - \frac{Q}{S_{\mathrm{e}}} \right) \exp \left( -\frac{S_{\mathrm{e}}}{V} t \right) + \frac{Q}{S_{\mathrm{e}}}
\end{align*}
です.
この式が理想的な排気曲線に相当します.
下グラフは,シミュレーションで追跡した真空槽内の平均圧力および配管入り口圧力の時間変化を,
実行排気速度として $S_{\mathrm{e}}$ を用いて現象論的に求めた排気曲線および
$S_{\mathrm{e}}^{\prime}$ を用いて理論的に求めた排気曲線と合わせてプロットしたものです.
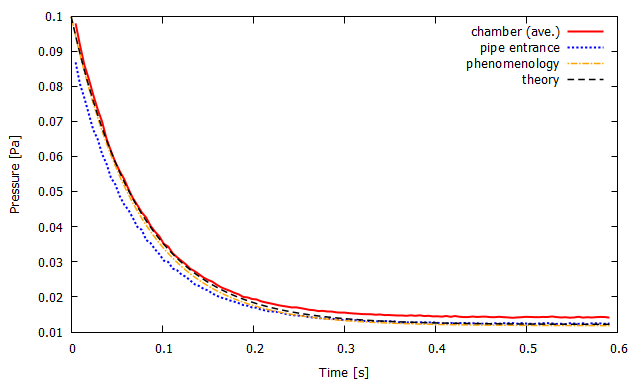
▲ 真空槽内の平均圧力(赤実線)および配管入り口の圧力(青点線)の時間変化と現象論的な排気曲線(橙鎖線)および理論的な排気曲線(黒破線).
真空槽内の平均圧力は,排気開始からしばらくの間はほとんど理想的に排気されますが, 徐々に排気効率が悪くなり,最終的な到達圧力は理想的な値 $Q/S_{\mathrm{e}}^{\prime}$ よりも大きくなっています. これは,上述した真空槽自体が持つコンダクタンスの影響等により, 理論値よりも排気されにくくなっている(=装置全体のコンダクタンスと比較して上部で評価した理論的なコンダクタンス値は過大である)ことが原因だと考えられます. 一方で,配管入り口圧力の到達圧力は,理論的に求めた配管のコンダクタンス値により評価される到達圧力 $Q/S_{\mathrm{e}}^{\prime}$ と高精度で一致していることが分かります.
*1 理論式と比較する際の分かりやすさのために理想的な排気条件を課しましたが,DSMC-Neutrals では流出境界条件として排気速度や圧力を指定することもできます.
*2 $20^{\circ}\!\mathrm{C}$ の空気のKnudsen数はおよそ $K_{\mathrm{n}}=6.6/(pL)$($p$ は圧力 $\mathrm{(Pa)}$,$L$ は代表長さ $\mathrm{(mm)}$)ですので, これをモデルAに対して計算すると真空槽中と配管中のいずれでも $K_{\mathrm{n}}\gt 1$ となりますので分子流としての振る舞いが期待されます. 後に理論式との比較を行うことを考えると,粘性流領域では表式が複雑になってしまいますので今回は簡単のために分子流領域の初期圧力からの排気を考えますが, より高圧からの排気シミュレーションであってもDSMC-Neutralsを使って行うことが可能です.
*3 理論的に求められる(厚みのない)オリフィスのコンダクタンスを基準にして,厚みの影響をClausing係数に押し付けた表式になります. ここでは,便宜上この式をして「理論式」と呼ぶことにします.
[1] S. Dashman, "Scientific foundation of vacuum technique", New York, John Wiley & Sons (1949).
配管の直列接続と並列接続Pipe Connected in Series and Parallel
次に,下図のように排気配管を直列接続した場合(計算モデルlong/B)と並列接続(計算モデルparallel/C)した場合について, 先ほどの計算モデルstandard/Aに対して比較してみましょう.
 |
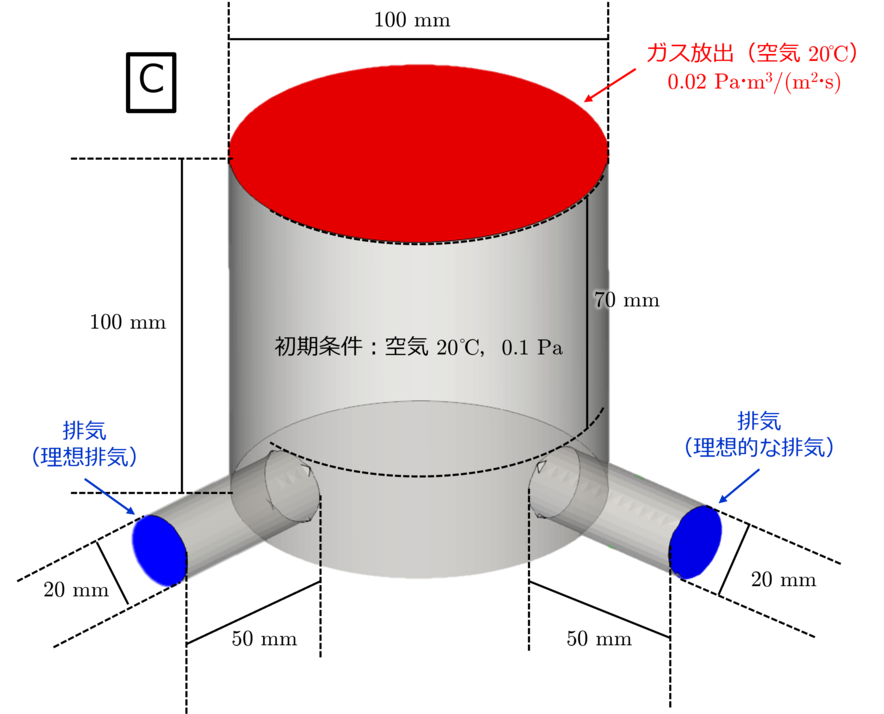 |
▲ 配管直列接続モデル(long/B)と配管並列接続モデル(parallel/C).
シミュレーションで追跡した真空槽内の平均圧力を計算モデルA,B,Cのそれぞれに対してプロットしたものが下グラフです.
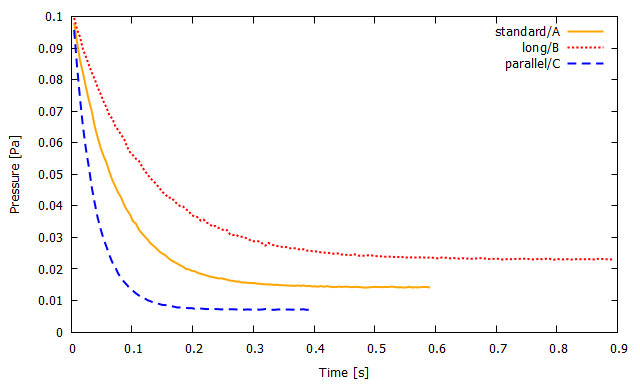
▲ 計算モデルA(橙実線),計算モデルB(赤点線),計算モデルC(青破線)における真空槽内の平均圧力.
配管を直列接続した場合の合成コンダクタンスはそれぞれのコンダクタンスの逆数の和の逆数であり,
同じコンダクタンス $C$ の配管を直列接続した場合の合成コンダクタンスは概算で $(1/2)C$ です.
一方で,並列接続した場合の合成コンダクタンスはそれぞれのコンダクタンスの単純和ですので,
同じコンダクタンス $C$ の配管を並列接続したならば合成コンダクタンスは $2C$ です.
グラフを見ると,確かにコンダクタンスが大きい(ガスが流れやすい)順に低い到達圧力が実現しています.
今度は,計算モデルBとCに着目して,シミュレーション結果と理論的に求めたコンダクタンスおよび実行排気速度を比べてみましょう.
ここで,理論的にコンダクタンスを求める際の注意点として,
実は今回の場合の計算モデルBについては長さ $50\ \mathrm{mm}$ の短円筒配管2本の合成コンダクタンスではなく,
長さ $100\ \mathrm{mm}$ の短円筒配管のコンダクタンスとして扱う必要があることに注意してください.
(精度を問わない大雑把な計算であれば上述の比較のように合成コンダクタンスの見積でも大丈夫です.)
さて,シミュレーションにより評価されたコンダクタンス $C$ および理論式*4から計算されたコンダクタンス $C_{\mathrm{f}}$ と,
対応する実行排気速度 $S_{\mathrm{e}}$ および $S_{\mathrm{e}}^{\prime}$ を比較してみましょう.
まず,計算モデルBについてまとめると,
\begin{align*}
C_{\mathrm{(B)}} &\sim 0.00624\ \mathrm{m^{3}/s},&
\quad
C_{\mathrm{t(B)}} &\sim 0.00725\ \mathrm{m^{3}/s},
\\
S_{e\mathrm{(B)}} &\sim 0.00577\ \mathrm{m^{3}/s},&
\quad
S_{\mathrm{e(B)}}^{\prime} &\sim 0.00662\ \mathrm{m^{3}/s}
\end{align*}
でした.
コンダクタンスの差異は相対的に $14\%$,絶対的に $0.0010\ \mathrm{m^{3}/s}$ でした.
実行排気速度の差異は相対的に $13\%$,絶対的に $0.00086\ \mathrm{m^{3}/s}$ でした.
次に,計算モデルCについてまとめると,
\begin{align*}
C_{\mathrm{(C)}} &\sim 0.0241\ \mathrm{m^{3}/s},&
\quad
C_{\mathrm{t(C)}} &\sim 0.0232\ \mathrm{m^{3}/s},
\\
S_{e\mathrm{(C)}} &\sim 0.0208\ \mathrm{m^{3}/s},&
\quad
S_{\mathrm{e(C)}}^{\prime} &\sim 0.0203\ \mathrm{m^{3}/s}
\end{align*}
でした.
コンダクタンスの差異は相対的に $3.9\%$,絶対的に $0.00090\ \mathrm{m^{3}/s}$ でした.
実行排気速度の差異は相対的に $2.2\%$,絶対的に $0.00046\ \mathrm{m^{3}/s}$ でした.
モデルBとCのそれぞれについて,
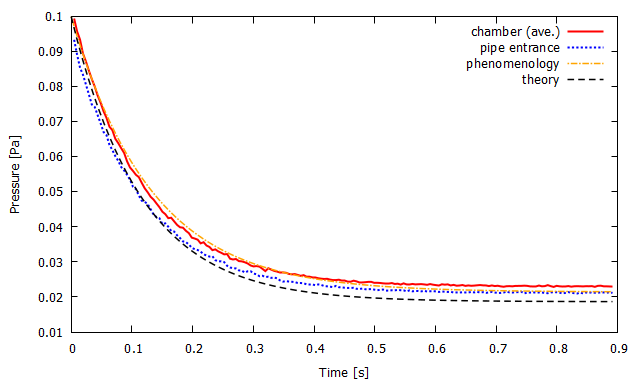
シミュレーションで追跡した真空槽内の平均圧力および配管入り口圧力の時間変化と現象論的および理論的な排気曲線を合わせてプロットしたものが下グラフです.
 |
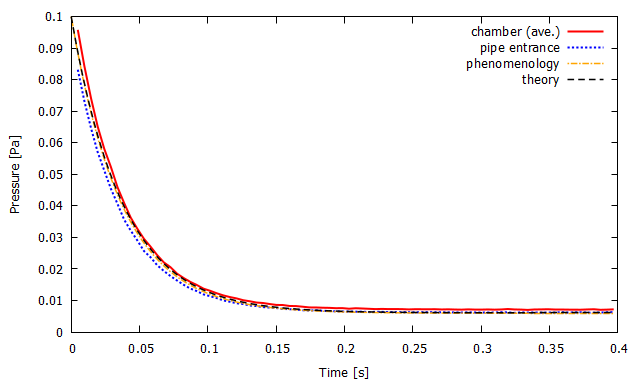 |
▲ 真空槽内の平均圧力(赤実線)および配管入り口の圧力(青点線)の時間変化と現象論的な排気曲線(橙鎖線)および理論的な排気曲線(黒破線). (左)計算モデルlong/B.(右)計算モデルparallel/C.
計算モデルBでは実際の排気性能が理論値よりも悪いことが分かります.
これについては後で考察を行います.
反対に,計算モデルCは理論値とよく一致しています.
一致の様子については計算モデルAと同じように,最初は真空槽内の平均圧力が理想的に排気され,
最終的には配管入り口の到達圧力が理論的な到達圧力とほとんど一致します.
*4 長さ $100\ \mathrm{mm}$ の短円筒配管で直径 $20\ \mathrm{mm}$ の短円筒配管のClausing係数は $K_{\mathrm{c}}=0.199$ としました. また,参考までに$50\ \mathrm{mm}$ の短円筒配管2本の合成コンダクタンスを計算すると, \begin{align*} C_{\mathrm{f}(100\ \mathrm{mm})} \simeq \frac{1}{2\times\frac{1}{C_{\mathrm{f}(50\ \mathrm{mm})}}} \sim 0.00579\ \mathrm{m^{3}/s} \end{align*} となります.
配管内のオリフィスの影響Effect of Orifice in Pipe
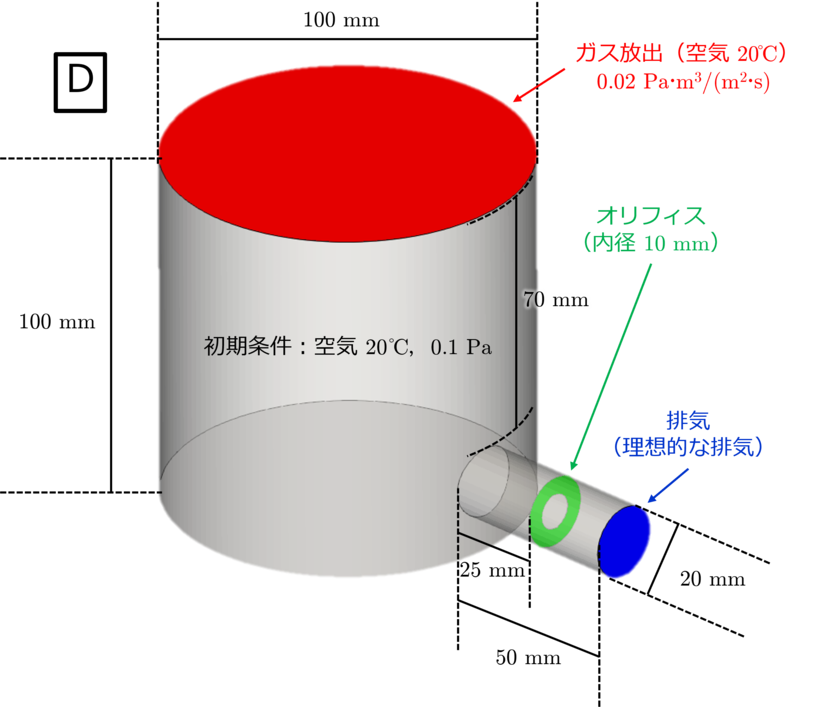
今度は,下図のように排気配管中にオリフィスを設置した場合について見てみましょう. 今回は,オリフィス内径が $10\ \mathrm{mm}$ の場合(計算モデルorifice (10mm)/D)と $15\ \mathrm{mm}$ の場合(計算モデルorifice (15mm)/E)の2計算モデルを考えます.
 |
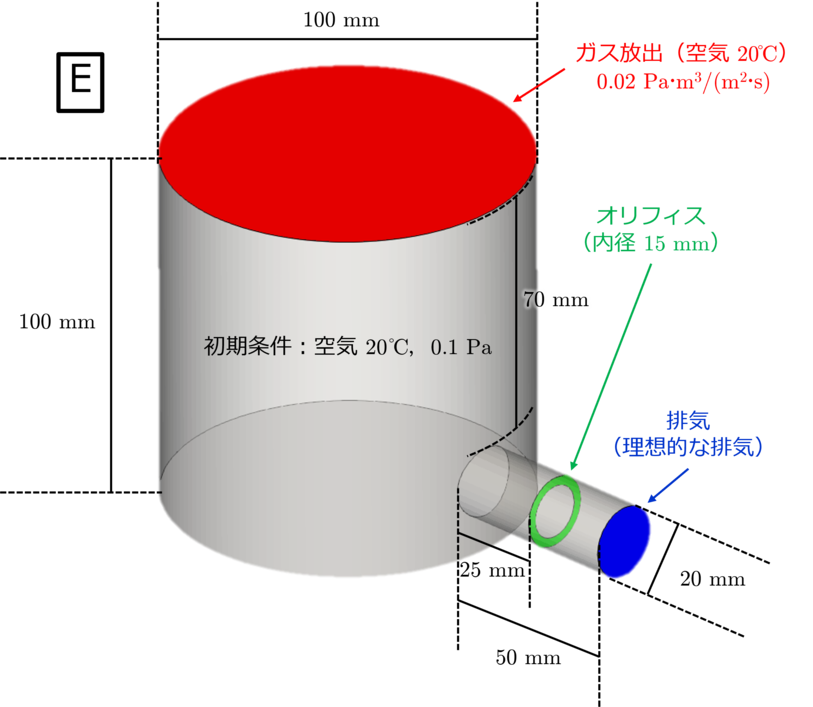 |
▲ オリフィス内径 $10\ \mathrm{mm}$ のモデル(orifice (10mm)/D)と $15\ \mathrm{mm}$ のモデル(orifice (15mm)/E).
最初に,真空槽内の平均圧力の時間変化について計算モデルstandard/Aのものと比較してみましょう.
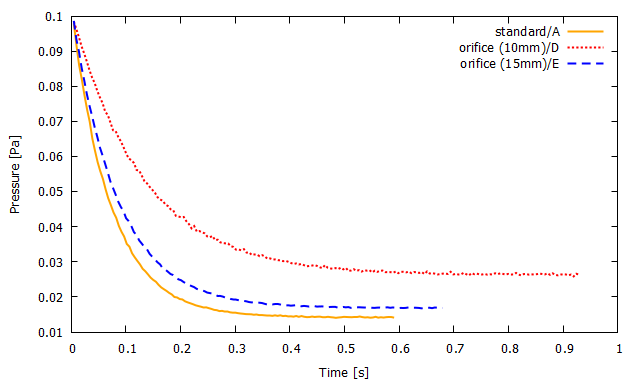
▲ 計算モデルA(橙実線),計算モデルD(赤点線),計算モデルE(青破線)における真空槽内の平均圧力.
オリフィス径が狭くなるほどコンダクタンスが小さくなり到達圧力が大きくなることは自明ではありますが,
シミュレーションによって具体的な排気曲線を得ることができました.
さて,これまでと同様に,シミュレーションにより評価されたコンダクタンス $C$ および理論式*4から計算されたコンダクタンス $C_{\mathrm{f}}$ と,
対応する実行排気速度 $S_{\mathrm{e}}$ および $S_{\mathrm{e}}^{\prime}$ を比較してみましょう.
ここで,配管中のオリフィスのコンダクタンスは
\begin{align*}
C_{\mathrm{f(orifice\ in\ pipe)}} = K\frac{116A}{1-A/A_{0}}
\end{align*}
と書けることが知られています[2].
ここで,$A$ はオリフィス孔の断面積 $\mathrm{(m^{2})}$,
$A_{0}$ は配管の断面積 $\mathrm{(m^{2})}$ です.
また,$K$ は上述のClausing係数と同様の補正係数で,配管内径とオリフィス内径の比に対して決まる量です.
まず計算モデルDについてまとめると,
\begin{align*}
C_{\mathrm{(D)}} &\sim 0.00560\ \mathrm{m^{3}/s},&
\quad
C_{\mathrm{t(D)}} &\sim 0.00607\ \mathrm{m^{3}/s},
\\
S_{e\mathrm{(D)}} &\sim 0.00524\ \mathrm{m^{3}/s},&
\quad
S_{\mathrm{e(D)}}^{\prime} &\sim 0.00565\ \mathrm{m^{3}/s}
\end{align*}
でした*5.
コンダクタンスの差異は相対的に $7.8\%$,絶対的に $0.00047\ \mathrm{m^{3}/s}$ でした.
実行排気速度の差異は相対的に $7.3\%$,絶対的に $0.00041\ \mathrm{m^{3}/s}$ でした.
次に,計算モデルEについてまとめると,
\begin{align*}
C_{\mathrm{(E)}} &\sim 0.00954\ \mathrm{m^{3}/s},&
\quad
C_{\mathrm{t(E)}} &\sim 0.00950\ \mathrm{m^{3}/s},
\\
S_{e\mathrm{(E)}} &\sim 0.00854\ \mathrm{m^{3}/s},&
\quad
S_{\mathrm{e(E)}}^{\prime} &\sim 0.00851\ \mathrm{m^{3}/s}
\end{align*}
でした*6.
コンダクタンスの差異は相対的に $0.36\%$,絶対的に $0.000034\ \mathrm{m^{3}/s}$ でした.
実行排気速度の差異は相対的に $0.32\%$,絶対的に $0.000027\ \mathrm{m^{3}/s}$ でした.
モデルDとEのそれぞれについて,
シミュレーションで追跡した真空槽内の平均圧力および配管入り口圧力の時間変化と現象論的および理論的な排気曲線を合わせてプロットしたものが下グラフです.
 |
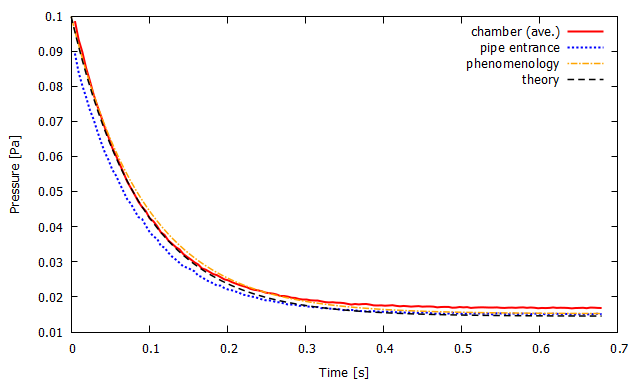 |
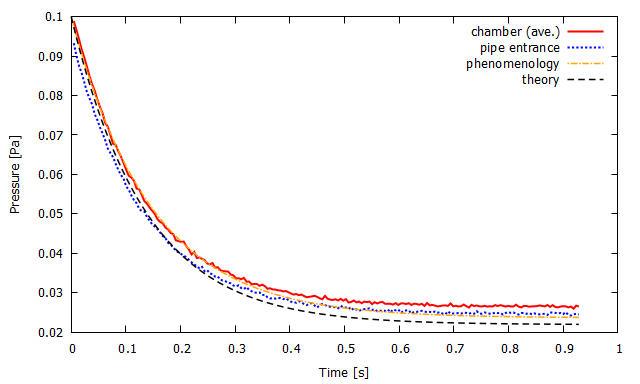
▲ 真空槽内の平均圧力(赤実線)および配管入り口の圧力(青点線)の時間変化と現象論的な排気曲線(橙鎖線)および理論的な排気曲線(黒破線). (左)計算モデルorifice (10mm)/D.(右)計算モデルorifice (15mm)/E.
計算モデルBと同様に,計算モデルDでは実際の排気性能が理論値よりも悪いことが分かります.
これについても計算モデルBと一緒に後で考察を行います.
反対に,計算モデルEは計算モデルCと同じように理論値とよく一致しています.
最初は真空槽内の平均圧力が理想的に排気され,
最終的には配管入り口の到達圧力が理論的な到達圧力とほとんど一致します.
*5 補正係数は $K\simeq 1.049$ としました.
*6 補正係数は $K\simeq 1.127$ としました.
[2] 熊谷寛夫,富永五郎,『真空の物理と応用』,裳華房 (1970).
バッフル(邪魔板)の影響Effect of Baffle
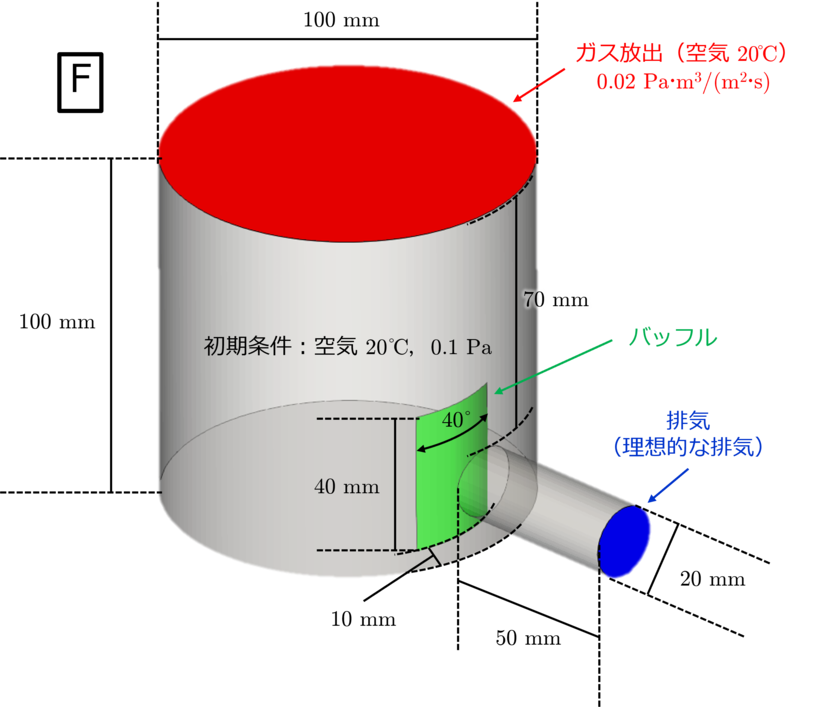
最後に,下図のようにバッフル(邪魔板)により配管の汚染(コンタミネーション)を防ぐような場合を想定した排気シミュレーションを行います. 今回はバッフルの取り付け位置を配管から $10\ \mathrm{mm}$ の場合(計算モデルbaffle/F)と $5\ \mathrm{mm}$ の場合(計算モデルcloser baffle/G)の2パターン考えます.
 |
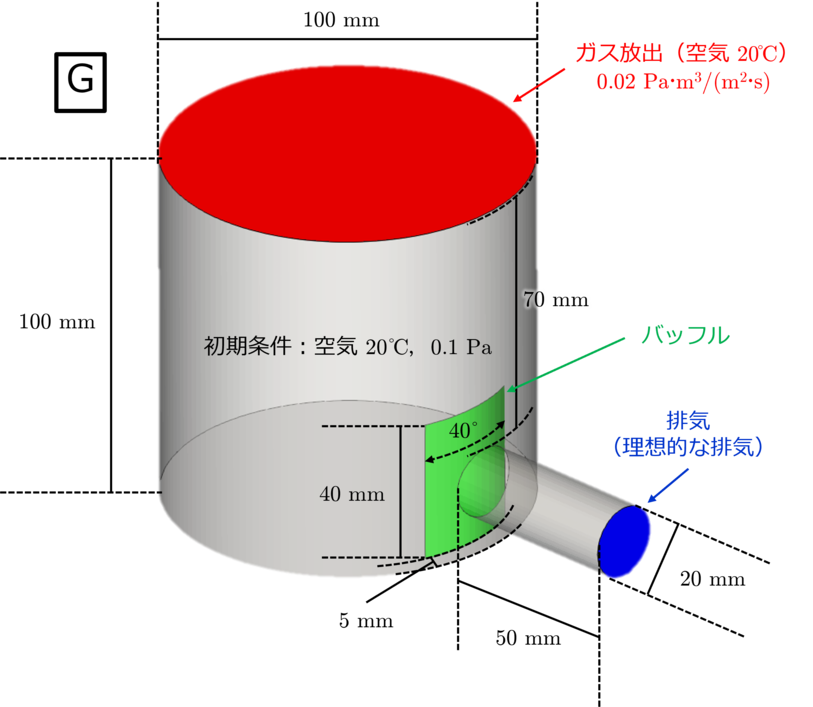 |
▲ 2種類のバッフル取り付けモデル(baffle/Fとcloser baffle/G).
今回は真空槽内の中央部圧力の時間変化について計算モデルstandard/Aのものと比較してみましょう.
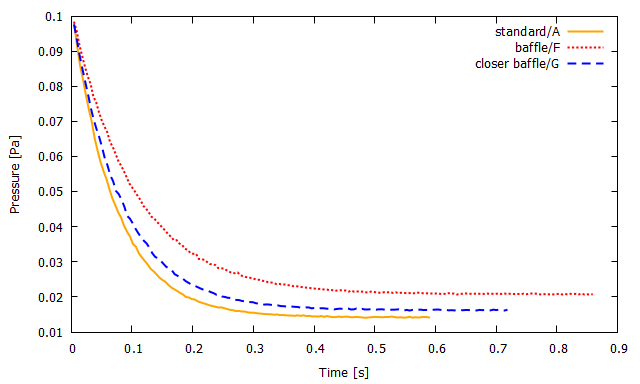
▲ 計算モデルA(橙実線),計算モデルF(赤点線),計算モデルG(青破線)における真空槽内の平均圧力.
配管入り口への流路が狭いほどコンダクタンスが小さくなることが推測されますが,
グラフを見ると確かにそのような結果が得られています.
さて,このようなモデルのコンダクタンスに関する理論的な表式は(おそらく)知られていませんので,
基本的にモンテカルロシミュレーションによって評価することが多いです.
DSMC-Neutralsを用いることで,任意形状の真空装置のコンダクタンスをシミュレーションにより評価することができます.
実際にシミュレーションにより評価した(配管+バッフル部の)コンダクタンスおよび実行排気速度は,計算モデルFに対して
\begin{align*}
C_{\mathrm{(F)}} \sim 0.00880\ \mathrm{m^{3}/s},
\quad
S_{e\mathrm{(F)}} \sim 0.00794\ \mathrm{m^{3}/s}
\end{align*}
であり,計算モデルGに対して
\begin{align*}
C_{\mathrm{(G)}} \sim 0.00672\ \mathrm{m^{3}/s},
\quad
S_{e\mathrm{(G)}} \sim 0.00621\ \mathrm{m^{3}/s}
\end{align*}
でした.
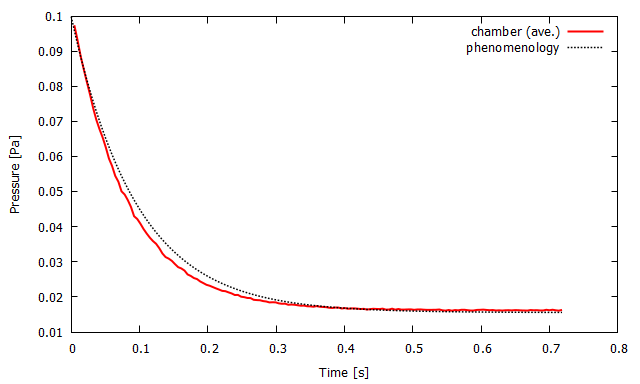
モデルFとGのそれぞれについて,
シミュレーションで追跡した真空槽内の平均圧力と現象論的な排気曲線を合わせてプロットすると下グラフが得られました.
 |
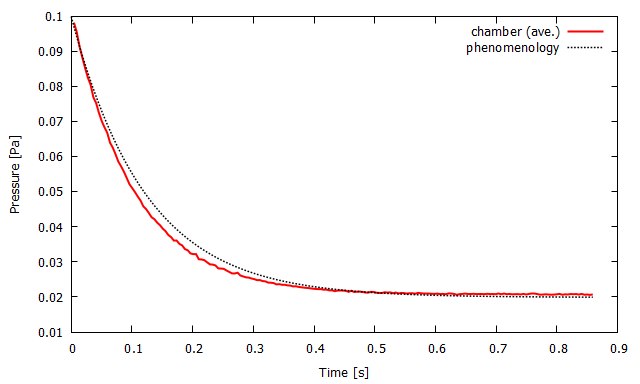 |
▲ 真空槽内の平均圧力(赤実線)の時間変化と現象論的な排気曲線(黒点線). (左)計算モデルbaffle/F.(右)計算モデルcloser baffle/G.
シミュレーションの生データとしての真空槽内平均圧力と排気曲線との間の差異に関しては, 真空槽内部において圧力分布があることなどに起因する真空槽の容積の評価に曖昧さがあることから生じていると考えられます.
考察とまとめConsideration and Summary
ここまでシミュレーション結果と理論的なコンダクタンス値や排気曲線を比較するなどしてきましたが,
全体的に両者の傾向が一致することは確かめられたものの,計算モデルBやDでは理論曲線からの差異が認められました.
最後に,その差異について考察してみましょう.
今,コンダクタンスの理論値 $C_{\mathrm{f}}$ とシミュレーション結果 $C$ との差異を
\begin{align*}
C_{\mathrm{f}} = C + \Delta C,\quad \text{i.e.} \quad \Delta C = C_{\mathrm{f}} - C
\end{align*}
のように $\Delta C$ で表すことにします.
このとき,理論値 $C$ と差異 $\Delta C$ の関係は下グラフのようになっていました.
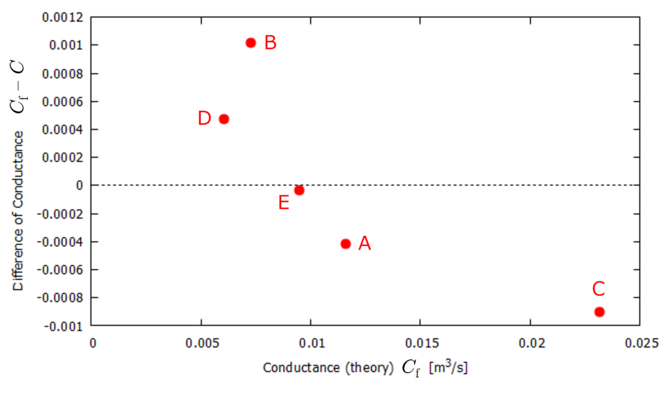
▲ コンダクタンスに関するシミュレーション結果と理論値との差異.
グラフを見ると $C$ と $\Delta C$ の間には負の相関があるようにも思えますが,データ点が少なく確かではありません.
しかしながら,少なくとも差異の大きさ $|\Delta C|$ については(現在のデータ範囲においては $O(10^{-3})$
よりも)極端に大きなオーダーになることは考えにくそうです.
(理論値とシミュレーション結果の相対的な差異がいきなり $50\%$ とか $100\%$ 以上になるようなことはないでしょう.)
一方で,排気曲線における重要な値である到達圧力(時刻 $t\to\infty$ での圧力)$P_{\mathrm{u}}$ について考えましょう.
到達圧力についてもシミュレーション結果と理論値との差異がありますので,
\begin{align*}
\Delta P_{\mathrm{u}} = P_{\mathrm{u}}^{\prime} - P_{\mathrm{u}}
= \frac{Q}{S_{\mathrm{e}}^{\prime}} - \frac{Q}{S_{\mathrm{e}}}
\end{align*}
と書けると考えます.
さて,誤差の伝播則より,
\begin{align*}
\left(\Delta P_{\mathrm{u}}\right)^{2}
= \left(\frac{\partial P_{\mathrm{u}}}{\partial C}\right)^{2} \left(\Delta C\right)^{2}
= \left(\frac{\partial}{\partial C}\frac{Q}{S_{\mathrm{e}}}\right)^{2}\left(\Delta C\right)^{2}
= \left(\frac{\partial}{\partial C}\frac{Q(S+C)}{SC}\right)^{2}\left(\Delta C\right)^{2}
= \left(\frac{Q}{C^{2}}\right)^{2}\left(\Delta C\right)^{2},
\quad
\text{i.e.}\quad \left|\Delta P_{\mathrm{u}}\right| = \left|\frac{Q}{C_{2}}\Delta C\right|
\end{align*}
であることが分かります.
この式が意味することは,$\Delta C$ の変化速度が $C^{2}$ の変化速度に打ち勝つような状況でなければ,
コンダクタンス値 $C$ が小さいほど到達圧力のシミュレーション結果と理論値との差異 $\Delta P_{\mathrm{u}}$ が大きいということです.
実際に,理論的なコンダクタンス値 $C$ と到達圧力差異 $\Delta P_{\mathrm{u}}$ をプロットすると下図のようになります.
これにより,計算モデルBやDにおいてシミュレーション結果と理論的な排気曲線との差異が比較的大きく,
それ以外のモデルではかなり良く一致している理由が定性的に説明できたかとおもいます.
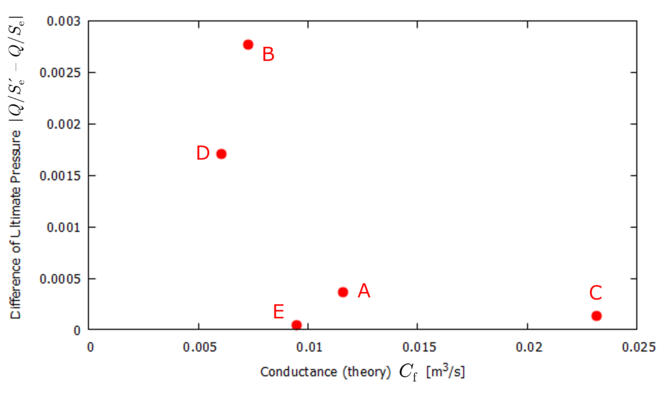
▲ 到達圧力に関するシミュレーション結果と理論値との差異.
以上のように,DSMC-Neutralsを使ってシミュレーションを行うことにより,
理論的な解析だけでは分からない部分や,理論が仮定している理想的な状況と実際の装置との差異について調べることができます.
また,理論的な見積もりができないバッフルを取り付けた真空装置のような複雑な装置のコンダクタンスについても評価することが可能です.
本コラムを読んで排気シミュレーションにご興味を持っていただけましたら幸いです.
少しでも気になる点がございましたらぜひともお気軽にお問い合わせください!
 |
上野 崚一郎 | 博士(理学) 1991年 広島県生まれ 2019年 ウェーブフロント入社 2019年 広島大学大学院理学研究科 博士後期課程修了 学生時代は数値シミュレーションを使った素粒子論(格子ゲージ理論)の研究に従事. 入社後は,専門職(エンジニア)として希薄気体解析・プラズマ解析ソフトウェアの開発をはじめとして, 解析コンサルティング業務や国内外のユーザー向けの技術サポート・トレーニングなどを担当. 最後までお読みいただきありがとうございます. お気づきの点や扱ってほしい話題がございましたらお気軽にお問い合わせください. |
